Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 143045 by 0731619 last updated on 09/Jun/21

Answered by Dwaipayan Shikari last updated on 09/Jun/21

$${\int }_0^1\frac{1-x^n}{1-x}dx=-\gamma +\psi (n+1)$$$$\underset{n\to 3}{\lim }\frac{-\gamma -1.833+\psi (n+1)}{\mathrm{\Gamma }(n+1)-6}\stackrel{Lhopital}{=}\frac{{\psi }^{\prime }(n+1)}{{\mathrm{\Gamma }}^{\prime }(n+1)}=\frac{{\psi }^{\prime }\left(4\right)}{\psi \left(4\right)\mathrm{\Gamma }\left(4\right)}$$$$\frac{\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{{(n+4)}^2}}{(\gamma +1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4})6}=\frac{\frac{{\pi }^2}{6}-\frac{1}{3^2}-\frac{1}{2^2}-1}{6\gamma +\frac{25}{2}}=\frac{6{\pi }^2-294}{216\gamma +450}$$

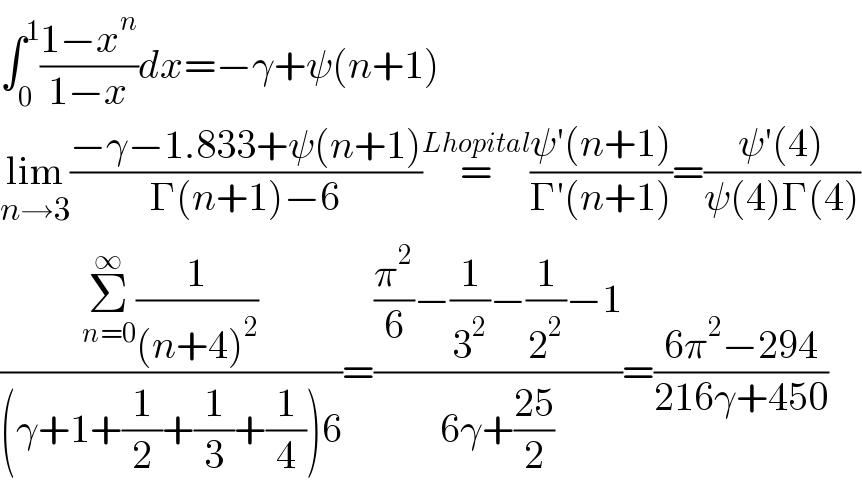
Commented by Canebulok last updated on 11/Jun/21

Hello mr. Payan , are you a mathematician?

Commented by Dwaipayan Shikari last updated on 11/Jun/21

Thanks for asking. I am a student and I am trying to learn my interest

Terms of Service

Privacy Policy

Contact: info@tinkutara.com