
Question and Answers Forum
Question Number 143071 by cesarL last updated on 09/Jun/21

Answered by TheSupreme last updated on 09/Jun/21
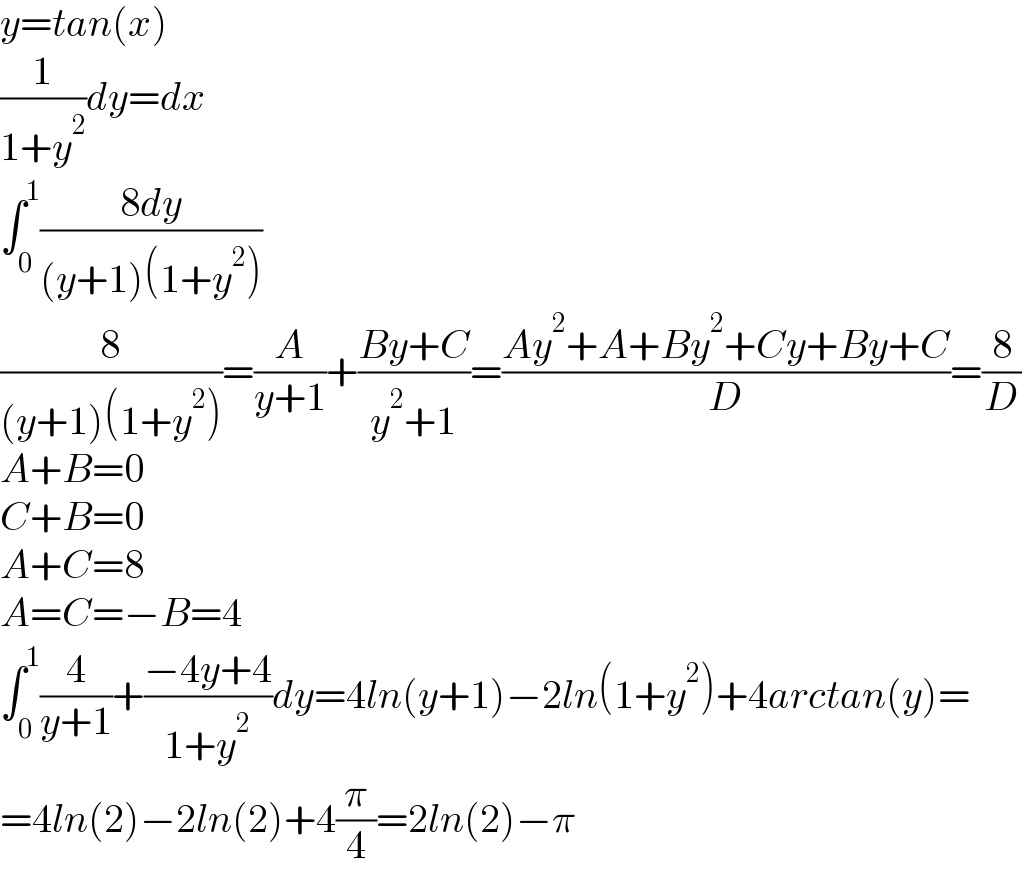
Answered by Olaf_Thorendsen last updated on 09/Jun/21
![C = ∫_0 ^(π/4) ((8cosx)/(cosx+sinx)) dx = ∫_0 ^(π/4) (8/(tanx+1)) dx S = ∫_0 ^(π/4) ((8sinx)/(cosx+sinx)) dx C+S = ∫_0 ^(π/4) 8dx = 2π (1) C−S = 8∫_0 ^(π/4) ((cosx−sinx)/(cosx+sinx)) dx C−S = 8[ln∣cox+sinx∣]_0 ^(π/4) C−S = 8ln(√2) = 4ln2 (2) (((1)+(2))/2) : C = π+2ln2](Q143079.png)
| ||
Question and Answers Forum | ||
Question Number 143071 by cesarL last updated on 09/Jun/21 | ||
 | ||
Answered by TheSupreme last updated on 09/Jun/21 | ||
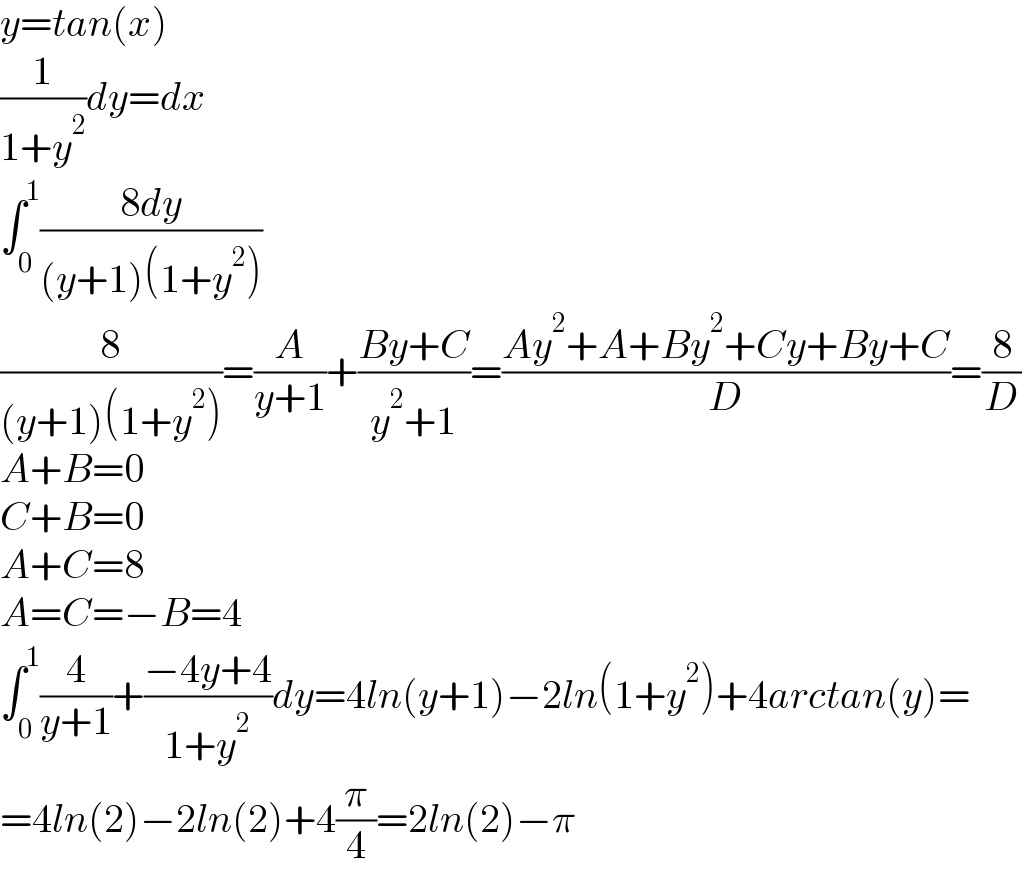 | ||
| ||
Answered by Olaf_Thorendsen last updated on 09/Jun/21 | ||
![C = ∫_0 ^(π/4) ((8cosx)/(cosx+sinx)) dx = ∫_0 ^(π/4) (8/(tanx+1)) dx S = ∫_0 ^(π/4) ((8sinx)/(cosx+sinx)) dx C+S = ∫_0 ^(π/4) 8dx = 2π (1) C−S = 8∫_0 ^(π/4) ((cosx−sinx)/(cosx+sinx)) dx C−S = 8[ln∣cox+sinx∣]_0 ^(π/4) C−S = 8ln(√2) = 4ln2 (2) (((1)+(2))/2) : C = π+2ln2](Q143079.png) | ||
| ||