Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 143100 by lapache last updated on 10/Jun/21

$$\int \sqrt{e^x+1}=.....???$$

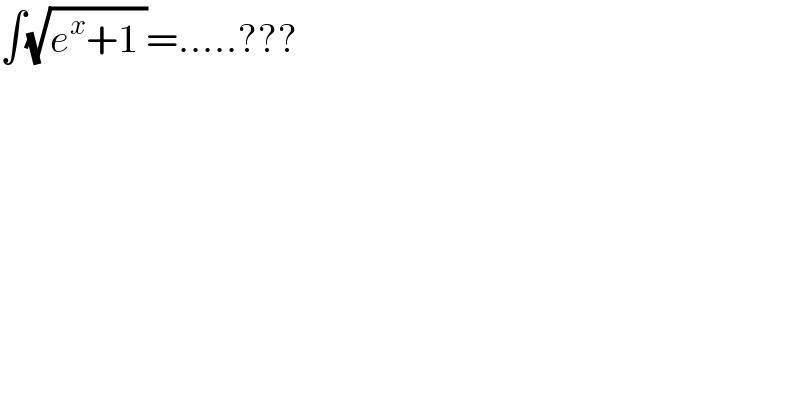
Answered by qaz last updated on 10/Jun/21

$$\int \sqrt{{\mathrm{e}}^{\mathrm{x}}+1}\mathrm{dx}$$$$=\int \sqrt{\mathrm{u}+1}\frac{\mathrm{du}}{\mathrm{u}}$$$$=\int \frac{\mathrm{u}+1}{\mathrm{u}\sqrt{\mathrm{u}+1}}\mathrm{du}$$$$=2\sqrt{\mathrm{u}+1}+\int \frac{\mathrm{du}}{{\mathrm{u}}^2\sqrt{\frac{1}{\mathrm{u}}+\frac{1}{{\mathrm{u}}^2}}}$$$$=2\sqrt{\mathrm{u}+1}-\int \frac{\mathrm{d}\left(\frac{1}{\mathrm{u}}\right)}{\sqrt{{(\frac{1}{\mathrm{u}}+\frac{1}{2})}^2-\frac{1}{4}}}$$$$=2\sqrt{\mathrm{u}+1}-\int \frac{\mathrm{d}\left[2(\frac{1}{\mathrm{u}}+\frac{1}{2})\right]}{\sqrt{[4{(\frac{1}{\mathrm{u}}+\frac{1}{2})}^2-1]}}$$$$=2\sqrt{\mathrm{u}+1}-\mathrm{arccosh}\left(2(\frac{1}{\mathrm{u}}+\frac{1}{2})\right)+\mathrm{C}$$$$=2\sqrt{{\mathrm{e}}^{\mathrm{x}}+1}-\mathrm{arccosh}\left(\frac{2+{\mathrm{e}}^{\mathrm{x}}}{{\mathrm{e}}^{\mathrm{x}}}\right)+\stackrel{}{\mathrm{C}}$$

Answered by MJS_new last updated on 10/Jun/21

$$\int \sqrt{{\mathrm{e}}^x+1}dx=$$$$[t=\sqrt{{\mathrm{e}}^x+1}\to dx=\frac{2\sqrt{{\mathrm{e}}^x+1}}{{\mathrm{e}}^x}dt]$$$$=2\int \frac{t^2}{t^2-1}dt=\int (2+\frac{1}{t-1}-\frac{1}{t+1})dt=$$$$=2t+\ln \frac{t-1}{t+1}=...$$$$=2\sqrt{{\mathrm{e}}^x+1}-x+\ln ({\mathrm{e}}^x+2-2\sqrt{{\mathrm{e}}^x+1})+C$$

Answered by pticantor last updated on 10/Jun/21

$$wokoooettuveuxlerizpourcassersahein$$$$tuvaslire?l^{\prime }heure$$

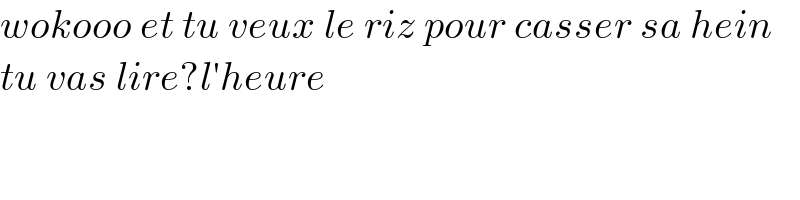
Answered by mathmax by abdo last updated on 11/Jun/21

$$\mathrm{I}=\int \sqrt{1+{\mathrm{e}}^{\mathrm{x}}}\mathrm{dx}\mathrm{we}\mathrm{do}\mathrm{the}\mathrm{changement}\sqrt{1+{\mathrm{e}}^{\mathrm{x}}}=\mathrm{t}\Rightarrow$$$$1+{\mathrm{e}}^{\mathrm{x}}={\mathrm{t}}^2\Rightarrow {\mathrm{e}}^{\mathrm{x}}={\mathrm{t}}^2-1\Rightarrow \mathrm{x}=\log ({\mathrm{t}}^2-1)\Rightarrow$$$$\mathrm{I}=\int \mathrm{t}\times \frac{2\mathrm{t}}{{\mathrm{t}}^2-1}\mathrm{dt}=2\int \frac{{\mathrm{t}}^2}{{\mathrm{t}}^2-1}\mathrm{dt}=2\int \frac{{\mathrm{t}}^2-1+1}{{\mathrm{t}}^2-1}\mathrm{dt}$$$$=2\mathrm{t}+\int \frac{2\mathrm{dt}}{{\mathrm{t}}^2-1}=2\mathrm{t}+\int (\frac{1}{\mathrm{t}-1}-\frac{1}{\mathrm{t}+1})\mathrm{dt}=2\mathrm{t}+\log \mid \frac{\mathrm{t}-1}{\mathrm{t}+1}\mid +\mathrm{C}$$$$\mathrm{I}=2\sqrt{1+{\mathrm{e}}^{\mathrm{x}}}+\log \mid \frac{\sqrt{1+{\mathrm{e}}^{\mathrm{x}}}-1}{\sqrt{1+{\mathrm{e}}^{\mathrm{x}}+1}}\mid +\mathrm{C}$$

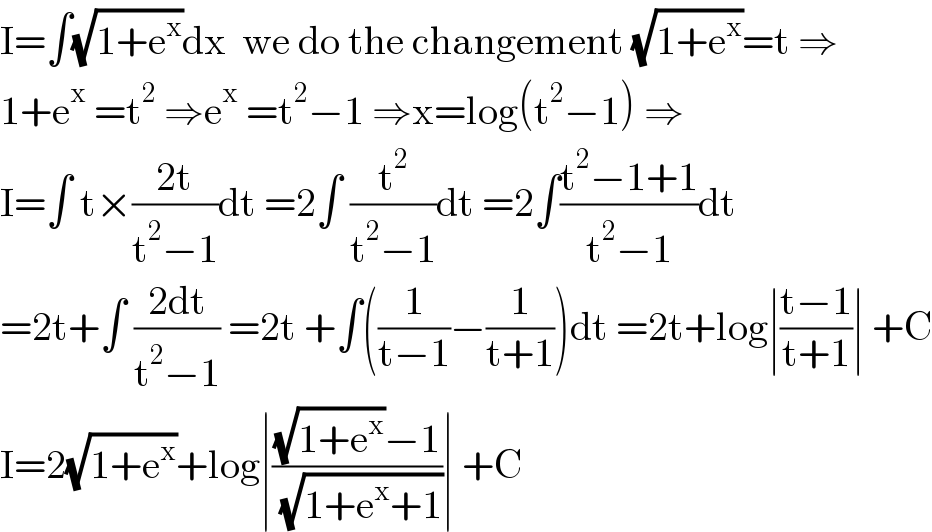
Commented by mathmax by abdo last updated on 11/Jun/21

$$\mathrm{typo}\mathrm{I}=2\sqrt{1+{\mathrm{e}}^{\mathrm{x}}}+\log \mid \frac{\sqrt{1+{\mathrm{e}}^{\mathrm{x}}}-1}{\sqrt{1+{\mathrm{e}}^{\mathrm{x}}}+1}\mid +\mathrm{C}$$

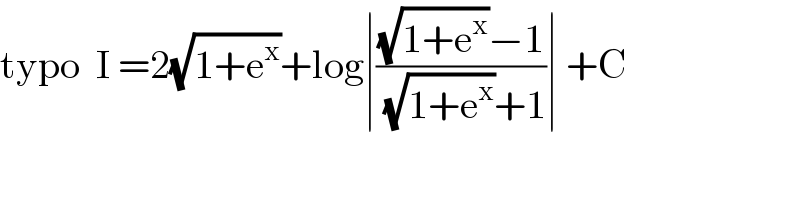
Answered by puissant last updated on 23/Aug/21

$$u=\sqrt{e^x+1}\to e^x=u^2-1\to x=ln(u^2-1)$$$$dx=\frac{2u}{u^2-1}du$$$$K=2\int \frac{u^2}{u^2-1}du$$$$K=2\int du+2\int \frac{1}{(u-1)(u+1)}du$$$$\Rightarrow K=2u+\int \frac{1}{u-1}du-\int \frac{1}{u+1}du$$$$\Rightarrow K=2u+ln\mid u-1\mid -ln\mid u+1\mid +C$$$$$$$$\therefore \because K=2\sqrt{e^x+1}+ln\mid \frac{\sqrt{e^x+1}-1}{\sqrt{e^x+1}+1}\mid +C..$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com