
Question and Answers Forum
Question Number 143190 by Ar Brandon last updated on 11/Jun/21

Commented by mohammad17 last updated on 11/Jun/21
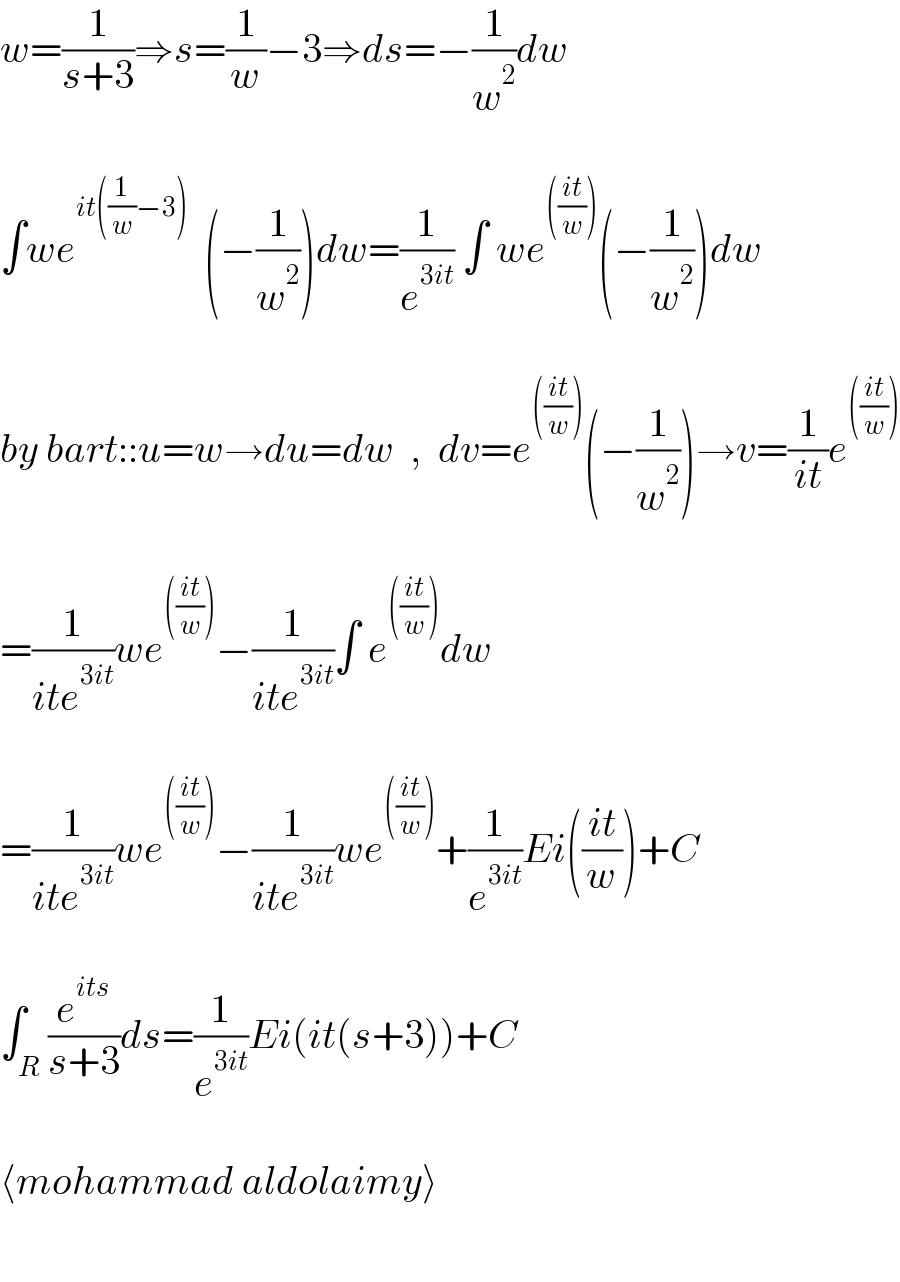
Commented by Ar Brandon last updated on 11/Jun/21
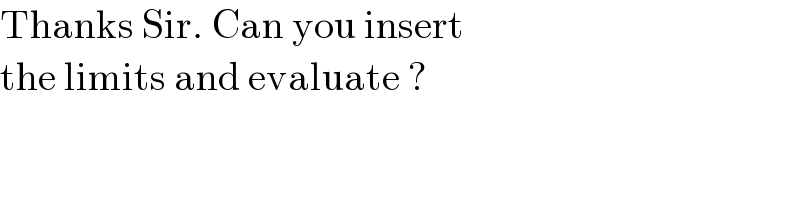
Answered by mathmax by abdo last updated on 11/Jun/21
![Φ=∫_(−∞) ^(+∞) (e^(itx) /(x+3))dx =∫_(−∞) ^0 (e^(itx) /(x+3))dx +∫_0 ^∞ (e^(itx) /(x+3))dx but ∫_(−∞) ^0 (e^(itx) /(x+3))dx =_(x=−u) ∫_0 ^∞ (e^(−itu) /(3−u))du =∫_0 ^∞ (e^(−itx) /(3−x))dx ⇒ Φ=∫_0 ^∞ (e^(itx) /(x+3))dx +∫_0 ^∞ (e^(−itx) /(3−x))dx [we have ∫_0 ^∞ (e^(itx) /(x+3))dx =∫_0 ^∞ (∫_0 ^∞ e^(−(x+3)z) dz)e^(itx) dx =∫_0 ^∞ (∫_0 ^∞ e^((−z+it)x) dx)e^(−3z) dz =∫_0 ^∞ ([(1/(−z+it))e^((−z+it)x) ]_0 ^∞ )e^(−3z) dz =∫_0 ^∞ ((1/(−z+it)))e^(−3z) dz =−∫_0 ^∞ ((1/(z−it)))e^(−3z) dz =−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ∫_0 ^∞ (e^(−itx) /(3−x))dx =∫_0 ^∞ (∫_0 ^∞ e^(−(3−x)z) dz)e^(−itx) dx =∫_0 ^∞ (∫_0 ^∞ e^((z−it)x) dx)e^(−3z) dz =∫_0 ^∞ ([(1/(z−it))e^((z−it)x) ]_0 ^∞ )e^(−3z) dz =∫_0 ^∞ (−(1/(z−it)))e^(−3z) dz =−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ⇒ Φ=−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz =−2∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ....be continued....](Q143202.png)
| ||
Question and Answers Forum | ||
Question Number 143190 by Ar Brandon last updated on 11/Jun/21 | ||
 | ||
Commented by mohammad17 last updated on 11/Jun/21 | ||
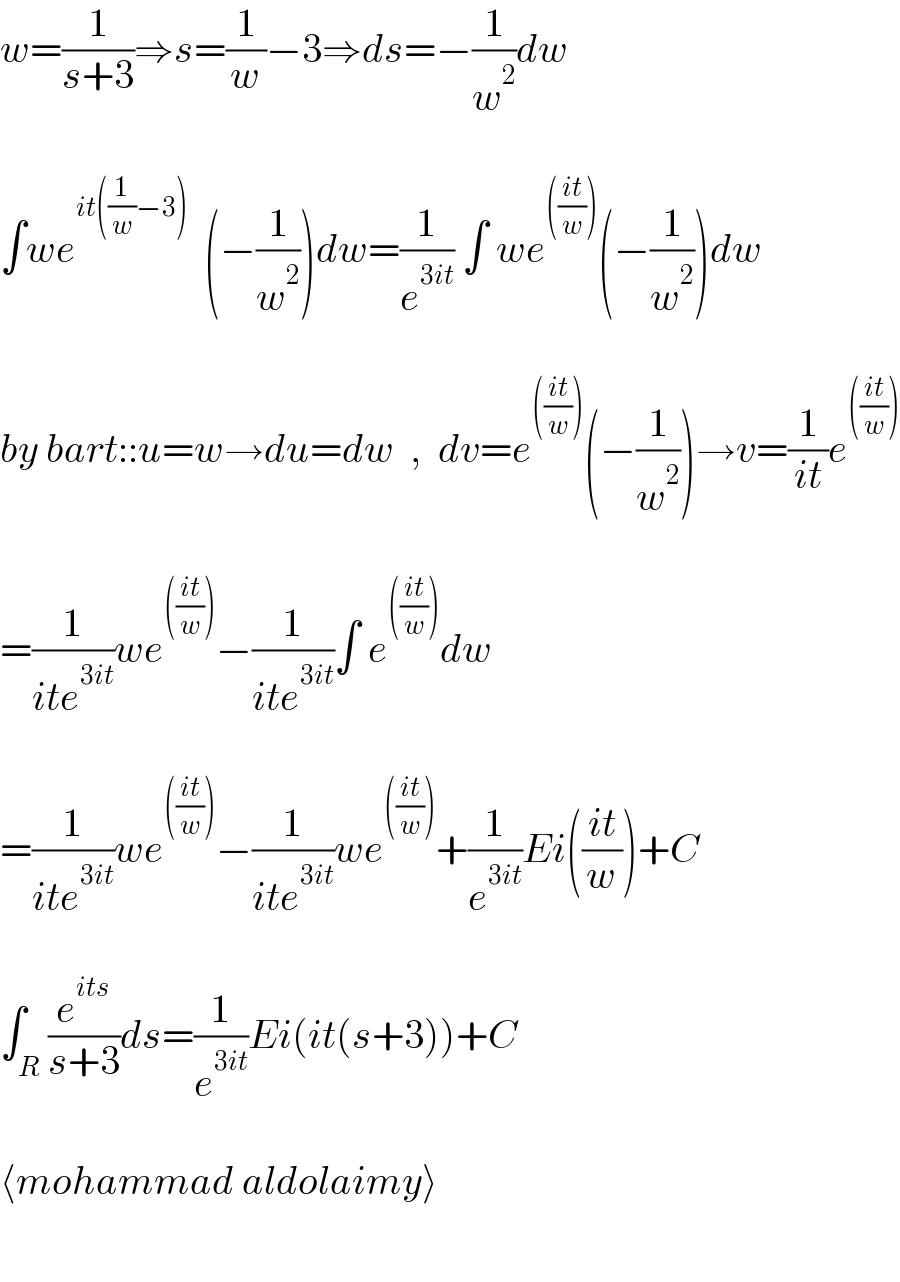 | ||
Commented by Ar Brandon last updated on 11/Jun/21 | ||
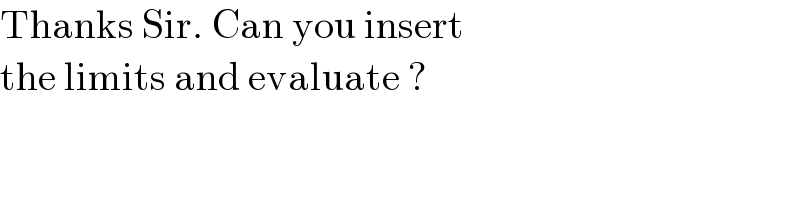 | ||
Answered by mathmax by abdo last updated on 11/Jun/21 | ||
![Φ=∫_(−∞) ^(+∞) (e^(itx) /(x+3))dx =∫_(−∞) ^0 (e^(itx) /(x+3))dx +∫_0 ^∞ (e^(itx) /(x+3))dx but ∫_(−∞) ^0 (e^(itx) /(x+3))dx =_(x=−u) ∫_0 ^∞ (e^(−itu) /(3−u))du =∫_0 ^∞ (e^(−itx) /(3−x))dx ⇒ Φ=∫_0 ^∞ (e^(itx) /(x+3))dx +∫_0 ^∞ (e^(−itx) /(3−x))dx [we have ∫_0 ^∞ (e^(itx) /(x+3))dx =∫_0 ^∞ (∫_0 ^∞ e^(−(x+3)z) dz)e^(itx) dx =∫_0 ^∞ (∫_0 ^∞ e^((−z+it)x) dx)e^(−3z) dz =∫_0 ^∞ ([(1/(−z+it))e^((−z+it)x) ]_0 ^∞ )e^(−3z) dz =∫_0 ^∞ ((1/(−z+it)))e^(−3z) dz =−∫_0 ^∞ ((1/(z−it)))e^(−3z) dz =−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ∫_0 ^∞ (e^(−itx) /(3−x))dx =∫_0 ^∞ (∫_0 ^∞ e^(−(3−x)z) dz)e^(−itx) dx =∫_0 ^∞ (∫_0 ^∞ e^((z−it)x) dx)e^(−3z) dz =∫_0 ^∞ ([(1/(z−it))e^((z−it)x) ]_0 ^∞ )e^(−3z) dz =∫_0 ^∞ (−(1/(z−it)))e^(−3z) dz =−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ⇒ Φ=−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz =−2∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ....be continued....](Q143202.png) | ||
| ||