
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 143259 by Mathspace last updated on 12/Jun/21
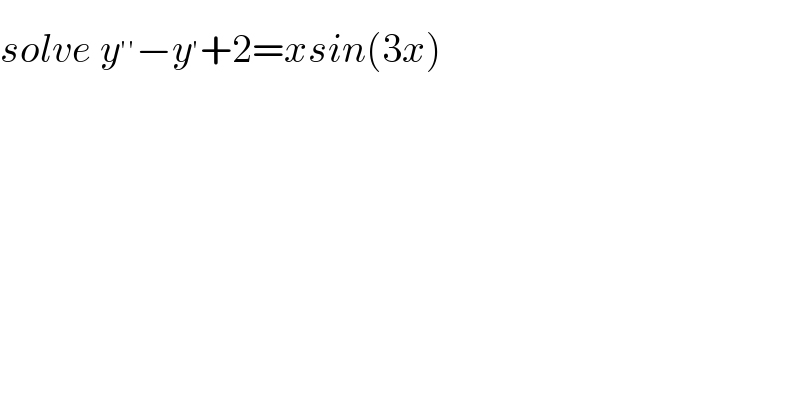
Answered by qaz last updated on 12/Jun/21
![y_p =(1/(D^2 −D))[xsin (3x)−2] =(1/(D−1))(−(1/3)xcos 3x+(1/9)sin 3x−2x) =−(1/3)∙(1/(D−1))(xcos 3x)+(1/9)∙(1/(D−1))(sin 3x)+2x+2 =−(1/3)(x−(1/(D−1)))(1/(D−1))cos 3x+(1/9)∙((D+1)/((−3^2 )−1))sin 3x+2x+2 =−(1/3)(x−(1/(D−1)))((D+1)/((−3^2 )−1))cos 3x−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))(x−(1/(D−1)))(−3sin 3x+cos 3x)−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))[−3xsin 3x+xcos 3x+((1+D)/(10))(−3sin 3x+cos 3x)]−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))[−3xsin 3x+xcos 3x−((4cos 3x+3sin 3x)/5)]−(1/(90))(3cos 3x+sin 3x)+2x+2 =−(1/(10))xsin 3x+(1/(30))xcos 3x−(3/(50))cos 3x−(7/(225))sin 3x+2x+2 ⇒y=C_1 +C_2 e^x −(1/(10))xsin 3x+(1/(30))xcos 3x−(3/(50))cos 3x−(7/(225))sin 3x+2x −−−−−−−−−−−−−−−−−−− y_p =(1/(D^2 −D))(xsin 3x−2) =(x−((2D−1)/(D^2 −D)))(1/(D^2 −D))(sin 3x)−(1/(D−1))(2x) =(x−((2D−1)/(D^2 −D)))((D^2 +D)/((−3^2 )^2 −(−3^2 )))(sin 3x)+2x+2 =(1/(90))(x−((2D−1)/(D^2 −D)))(3cos 3x−9sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(30))∙((2D−1)/(D^2 −D))(cos 3x−3sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(30))∙(((2D−1)(D^2 +D))/((−3^2 )^2 −(−3^2 )))(cos 3x−3sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(450))(2D−1)(4sin 3x−3cos 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(450))(27cos 3x+14sin 3x)+2x+2 ⇒y=C_1 +C_2 e^x +(x/(30))(cos 3x−3sin 3x)−(1/(450))(27cos 3x+14sin 3x)+2x](Q143291.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 143259 by Mathspace last updated on 12/Jun/21 | ||
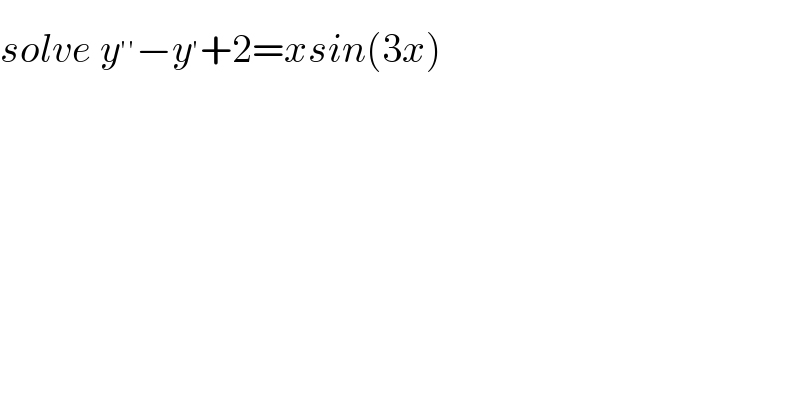 | ||
Answered by qaz last updated on 12/Jun/21 | ||
![y_p =(1/(D^2 −D))[xsin (3x)−2] =(1/(D−1))(−(1/3)xcos 3x+(1/9)sin 3x−2x) =−(1/3)∙(1/(D−1))(xcos 3x)+(1/9)∙(1/(D−1))(sin 3x)+2x+2 =−(1/3)(x−(1/(D−1)))(1/(D−1))cos 3x+(1/9)∙((D+1)/((−3^2 )−1))sin 3x+2x+2 =−(1/3)(x−(1/(D−1)))((D+1)/((−3^2 )−1))cos 3x−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))(x−(1/(D−1)))(−3sin 3x+cos 3x)−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))[−3xsin 3x+xcos 3x+((1+D)/(10))(−3sin 3x+cos 3x)]−(1/(90))(3cos 3x+sin 3x)+2x+2 =(1/(30))[−3xsin 3x+xcos 3x−((4cos 3x+3sin 3x)/5)]−(1/(90))(3cos 3x+sin 3x)+2x+2 =−(1/(10))xsin 3x+(1/(30))xcos 3x−(3/(50))cos 3x−(7/(225))sin 3x+2x+2 ⇒y=C_1 +C_2 e^x −(1/(10))xsin 3x+(1/(30))xcos 3x−(3/(50))cos 3x−(7/(225))sin 3x+2x −−−−−−−−−−−−−−−−−−− y_p =(1/(D^2 −D))(xsin 3x−2) =(x−((2D−1)/(D^2 −D)))(1/(D^2 −D))(sin 3x)−(1/(D−1))(2x) =(x−((2D−1)/(D^2 −D)))((D^2 +D)/((−3^2 )^2 −(−3^2 )))(sin 3x)+2x+2 =(1/(90))(x−((2D−1)/(D^2 −D)))(3cos 3x−9sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(30))∙((2D−1)/(D^2 −D))(cos 3x−3sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(30))∙(((2D−1)(D^2 +D))/((−3^2 )^2 −(−3^2 )))(cos 3x−3sin 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(450))(2D−1)(4sin 3x−3cos 3x)+2x+2 =(x/(30))(cos 3x−3sin 3x)−(1/(450))(27cos 3x+14sin 3x)+2x+2 ⇒y=C_1 +C_2 e^x +(x/(30))(cos 3x−3sin 3x)−(1/(450))(27cos 3x+14sin 3x)+2x](Q143291.png) | ||
| ||