
Question and Answers Forum
Question Number 143326 by SOMEDAVONG last updated on 13/Jun/21
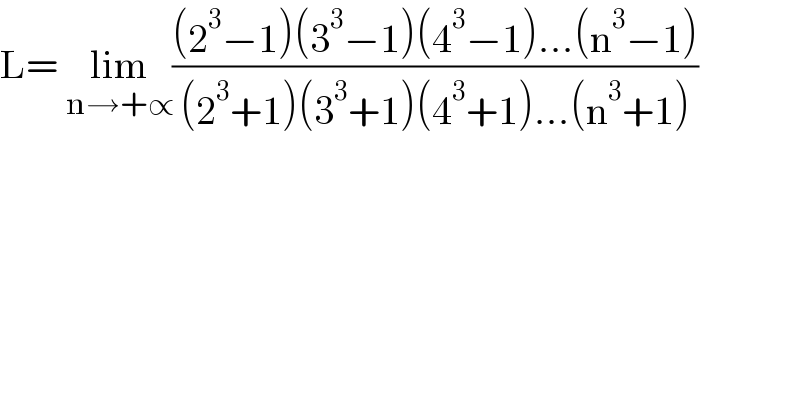
Answered by gsk2684 last updated on 13/Jun/21

| ||
Question and Answers Forum | ||
Question Number 143326 by SOMEDAVONG last updated on 13/Jun/21 | ||
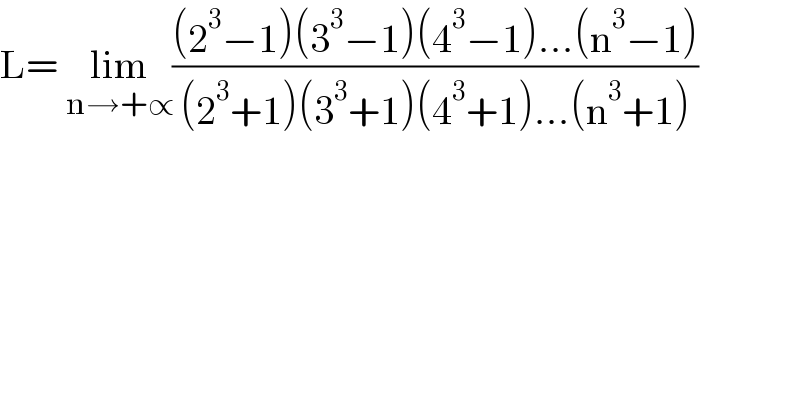 | ||
Answered by gsk2684 last updated on 13/Jun/21 | ||
 | ||
| ||