Question Number 143368 by mr W last updated on 13/Jun/21
Commented by mr W last updated on 13/Jun/21
![This is a solved old question (Q142207). The answer is a_n =(((√2)[((√2)+1)^(2(2n−1)) +1])/( ((√2)+1)^(2(2n−1)) −1)) Any other ways to solve?](Q143379.png)
$${This}\:{is}\:{a}\:{solved}\:{old}\:{question}\: \\ $$$$\left({Q}\mathrm{142207}\right).\:{The}\:{answer}\:{is} \\ $$$${a}_{{n}} =\frac{\sqrt{\mathrm{2}}\left[\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)} +\mathrm{1}\right]}{\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)} −\mathrm{1}} \\ $$$${Any}\:{other}\:{ways}\:{to}\:{solve}? \\ $$
Answered by mr W last updated on 13/Jun/21
![here a new way. a_(n+1) =((a_n +(4/3))/(1+(2/3)a_n )) λa_(n+1) =((λa_n +((4λ)/3))/(1+(2/(3λ))×λa_n )) let tan θ_n =λa_n and ((4λ)/3)=−(2/(3λ))=tan α ...(I) tan θ_(n+1) =((tan θ_n +tan α)/(1−tan θ_n tan α))=tan (θ_n +α) ⇒θ_(n+1) =θ_n +α ⇒θ_n =θ_1 +(n−1)α tan θ_n =((tan θ_1 +tan (n−1)α)/(1−tan θ_1 tan (n−1)α)) λa_n =((λa_1 +tan (n−1)α)/(1−λa_1 tan (n−1)α)) ⇒a_n =((a_1 +(1/λ)tan (n−1)α)/(1−a_1 λtan (n−1)α)) ...(II) from (I): ((4λ)/3)=−(2/(3λ)) λ^2 =−(1/2) ⇒λ=±(i/( (√2))) we take λ=(i/( (√2))) tan α=((4λ)/3)=((2(√2)i)/3) ⇒α=(tanh^(−1) ((2(√2))/3))i tan (n−1)α=[tanh {(n−1)tanh^(−1) ((2(√2))/3)}]i put into (II): a_n =((2+((√2)/i)×[tanh {(n−1)tanh^(−1) ((2(√2))/3)}]i)/(1−2×(i/( (√2)))×[tanh {(n−1)tanh^(−1) ((2(√2))/3)}]i)) a_n =((2+(√2)[tanh {(n−1)tanh^(−1) ((2(√2))/3)}])/(1+(√2)[tanh {(n−1)tanh^(−1) ((2(√2))/3)}])) tanh^(−1) ((2(√2))/3)=(1/2)ln ((1+((2(√2))/3))/(1−((2(√2))/3)))=2ln ((√2)+1) tanh {(n−1)tanh^(−1) ((2(√2))/3)} =tanh {ln ((√2)+1)^(2(n−1)) } =((((√2)+1)^(4(n−1)) −1)/(((√2)+1)^(4(n−1)) +1)) =1−(2/(((√2)+1)^(4(n−1)) +1)) a_n =((2+(√2)[1−(2/(((√2)+1)^(4(n−1)) +1))])/(1+(√2)[1−(2/(((√2)+1)^(4(n−1)) +1))])) a_n =(((√2)((√2)+1)−((2(√2))/(((√2)+1)^(4(n−1)) +1)))/( (√2)+1−((2(√2))/(((√2)+1)^(4(n−1)) +1)))) a_n =(((√2)((√2)+1)+(√2)((√2)+1)^(4(n−1)+1) −2(√2))/( (√2)+1+((√2)+1)^(4(n−1)+1) −2(√2))) a_n =(((√2)[((√2)−1)+((√2)+1)^(4(n−1)+1) ])/( ((√2)+1)^(4(n−1)+1) −((√2)−1))) a_n =(((√2)[((√2)+1)^(2(2n−1)) +1])/( ((√2)+1)^(2(2n−1)) −1))](Q143394.png)
$${here}\:{a}\:{new}\:{way}. \\ $$$${a}_{{n}+\mathrm{1}} =\frac{{a}_{{n}} +\frac{\mathrm{4}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{a}_{{n}} } \\ $$$$\lambda{a}_{{n}+\mathrm{1}} =\frac{\lambda{a}_{{n}} +\frac{\mathrm{4}\lambda}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}\lambda}×\lambda{a}_{{n}} } \\ $$$${let}\:\mathrm{tan}\:\theta_{{n}} =\lambda{a}_{{n}} \:{and} \\ $$$$\frac{\mathrm{4}\lambda}{\mathrm{3}}=−\frac{\mathrm{2}}{\mathrm{3}\lambda}=\mathrm{tan}\:\alpha\:\:\:\:\:...\left({I}\right) \\ $$$$\mathrm{tan}\:\theta_{{n}+\mathrm{1}} =\frac{\mathrm{tan}\:\theta_{{n}} +\mathrm{tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:\theta_{{n}} \mathrm{tan}\:\alpha}=\mathrm{tan}\:\left(\theta_{{n}} +\alpha\right) \\ $$$$\Rightarrow\theta_{{n}+\mathrm{1}} =\theta_{{n}} +\alpha \\ $$$$\Rightarrow\theta_{{n}} =\theta_{\mathrm{1}} +\left({n}−\mathrm{1}\right)\alpha \\ $$$$\mathrm{tan}\:\theta_{{n}} =\frac{\mathrm{tan}\:\theta_{\mathrm{1}} +\mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha}{\mathrm{1}−\mathrm{tan}\:\theta_{\mathrm{1}} \mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha} \\ $$$$\lambda{a}_{{n}} =\frac{\lambda{a}_{\mathrm{1}} +\mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha}{\mathrm{1}−\lambda{a}_{\mathrm{1}} \mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha} \\ $$$$\Rightarrow{a}_{{n}} =\frac{{a}_{\mathrm{1}} +\frac{\mathrm{1}}{\lambda}\mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha}{\mathrm{1}−{a}_{\mathrm{1}} \lambda\mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha}\:\:\:...\left({II}\right) \\ $$$${from}\:\left({I}\right): \\ $$$$\frac{\mathrm{4}\lambda}{\mathrm{3}}=−\frac{\mathrm{2}}{\mathrm{3}\lambda} \\ $$$$\lambda^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\lambda=\pm\frac{{i}}{\:\sqrt{\mathrm{2}}} \\ $$$${we}\:{take}\:\lambda=\frac{{i}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{4}\lambda}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}{i}}{\mathrm{3}} \\ $$$$\Rightarrow\alpha=\left(\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right){i} \\ $$$$\mathrm{tan}\:\left({n}−\mathrm{1}\right)\alpha=\left[\mathrm{tanh}\:\left\{\left({n}−\mathrm{1}\right)\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right\}\right]{i} \\ $$$${put}\:{into}\:\left({II}\right): \\ $$$${a}_{{n}} =\frac{\mathrm{2}+\frac{\sqrt{\mathrm{2}}}{{i}}×\left[\mathrm{tanh}\:\left\{\left({n}−\mathrm{1}\right)\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right\}\right]{i}}{\mathrm{1}−\mathrm{2}×\frac{{i}}{\:\sqrt{\mathrm{2}}}×\left[\mathrm{tanh}\:\left\{\left({n}−\mathrm{1}\right)\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right\}\right]{i}} \\ $$$${a}_{{n}} =\frac{\mathrm{2}+\sqrt{\mathrm{2}}\left[\mathrm{tanh}\:\left\{\left({n}−\mathrm{1}\right)\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right\}\right]}{\mathrm{1}+\sqrt{\mathrm{2}}\left[\mathrm{tanh}\:\left\{\left({n}−\mathrm{1}\right)\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right\}\right]} \\ $$$$\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}}=\mathrm{2ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\mathrm{tanh}\:\left\{\left({n}−\mathrm{1}\right)\mathrm{tanh}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right\} \\ $$$$=\mathrm{tanh}\:\left\{\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}\left({n}−\mathrm{1}\right)} \right\} \\ $$$$=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} −\mathrm{1}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} +\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\mathrm{2}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} +\mathrm{1}} \\ $$$${a}_{{n}} =\frac{\mathrm{2}+\sqrt{\mathrm{2}}\left[\mathrm{1}−\frac{\mathrm{2}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} +\mathrm{1}}\right]}{\mathrm{1}+\sqrt{\mathrm{2}}\left[\mathrm{1}−\frac{\mathrm{2}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} +\mathrm{1}}\right]} \\ $$$${a}_{{n}} =\frac{\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} +\mathrm{1}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left({n}−\mathrm{1}\right)} +\mathrm{1}}} \\ $$$${a}_{{n}} =\frac{\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)+\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{1}} −\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{1}} −\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${a}_{{n}} =\frac{\sqrt{\mathrm{2}}\left[\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{1}} \right]}{\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{4}\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{1}} −\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)} \\ $$$${a}_{{n}} =\frac{\sqrt{\mathrm{2}}\left[\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}\left(\mathrm{2n}−\mathrm{1}\right)} +\mathrm{1}\right]}{\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}\left(\mathrm{2n}−\mathrm{1}\right)} −\mathrm{1}} \\ $$
Answered by mindispower last updated on 14/Jun/21
$${let}\:{f}\left({x}\right)=\frac{\mathrm{3}{x}+\mathrm{4}}{\mathrm{2}{x}+\mathrm{3}},{f}^{{n}} \left({x}\right)={fofo}.....{f}\left({x}\right) \\ $$$${n}\:{composition}\:{of}\:{f} \\ $$$${f}^{{n}} \left({x}\right)=\frac{{a}_{{n}} {x}+{b}_{{n}} }{{c}_{{n}} {x}+{d}_{{n}} } \\ $$$${A}=\begin{pmatrix}{\mathrm{3}\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{4}\:\:\:\:\:\:\mathrm{3}}\end{pmatrix},{A}^{{n}} =\begin{pmatrix}{{a}_{{n}} \:\:\:\:\:{c}_{{n}} }\\{{b}_{{n}} \:\:\:\:\:\:{d}_{{n}} }\end{pmatrix}...{claimt} \\ $$$${A}^{\mathrm{1}} ={A}\:{true} \\ $$$${A}^{{n}+\mathrm{1}} ={A}.{A}^{{n}} =\begin{pmatrix}{\mathrm{3}{a}_{{n}} +\mathrm{2}{b}_{{n}} \:\:\:\mathrm{2}{d}_{{n}} +\mathrm{3}{c}_{{n}} }\\{\mathrm{4}{b}_{{n}} +\mathrm{3}{d}_{{n}} \:\:\:\mathrm{4}{c}_{{n}} +\mathrm{3}{d}_{{n}} }\end{pmatrix} \\ $$$${f}^{{n}+\mathrm{1}} \left({x}\right)={f}^{{n}} {of}=\frac{{a}_{{n}} .\frac{\mathrm{3}{x}+\mathrm{4}}{\mathrm{2}{x}+\mathrm{3}}+{b}_{{n}} }{{c}_{{n}} .\frac{\mathrm{3}{x}+\mathrm{4}}{\mathrm{2}{x}+\mathrm{3}}+{d}_{{n}} } \\ $$$$=\frac{\left(\mathrm{3}{a}_{{n}} +\mathrm{2}{b}_{{n}} \right){x}+\mathrm{4}{a}_{{n}} +\mathrm{3}{b}_{{n}} }{\left(\mathrm{3}{c}_{{n}} +\mathrm{2}{d}_{{n}} \right){x}+\mathrm{4}{c}_{{n}} +\mathrm{3}{d}_{{n}} }...{True} \\ $$$${det}\left({A}−{xI}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{3}−{x}\right)^{\mathrm{2}} −\mathrm{8}=\mathrm{0}\Rightarrow{x}\in\left\{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{3};\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right\} \\ $$$$\left({A}−\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right){I}_{\mathrm{2}} \right){u}=\mathrm{0} \\ $$$$\Rightarrow{u}\left({x},{y}\right)\mid−\mathrm{2}\sqrt{\mathrm{2}}{x}+\mathrm{2}{y}=\mathrm{0}\Rightarrow{u}\left(\mathrm{1},\sqrt{\mathrm{2}}\right) \\ $$$$\left({A}−\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)\right){u}=\mathrm{0}\Rightarrow\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{2}}\right){x}+\mathrm{2}{y}=\mathrm{0} \\ $$$${u}\left(\mathrm{1},\mathrm{3}−\sqrt{\mathrm{2}}\right) \\ $$$${P}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}}\\{\sqrt{\mathrm{2}}\:\:\:\:\mathrm{3}−\sqrt{\mathrm{2}}}\end{pmatrix} \\ $$$${P}^{−} =\frac{\mathrm{1}}{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\begin{pmatrix}{\mathrm{3}−\sqrt{\mathrm{2}}\:\:\:\:\:\:−\mathrm{1}\:\:\:}\\{−\sqrt{\mathrm{2}}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}^{{n}} =\frac{\mathrm{1}}{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\sqrt{\mathrm{2}}\:\:\:\:\:\:\mathrm{3}−\sqrt{\mathrm{2}}}\end{pmatrix}.\begin{pmatrix}{\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{3}\right)^{{n}} \:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{{n}} }\end{pmatrix}.\begin{pmatrix}{\mathrm{3}−\sqrt{\mathrm{2}}\:\:\:\:\:−\mathrm{1}}\\{−\sqrt{\mathrm{2}}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${this}\:{give}\:{us}\:{a}_{{n}} ,{b}_{{n}} ,{c}_{{n}} ,{d}_{{n}} \\ $$$${then}\:{f}^{{n}} \left({x}\right) \\ $$$${a}_{{n}+\mathrm{1}} ={f}^{{n}} \left(\mathrm{2}\right),{f}^{{o}} ={Id},{f}\left({x}\right)={x} \\ $$$$ \\ $$
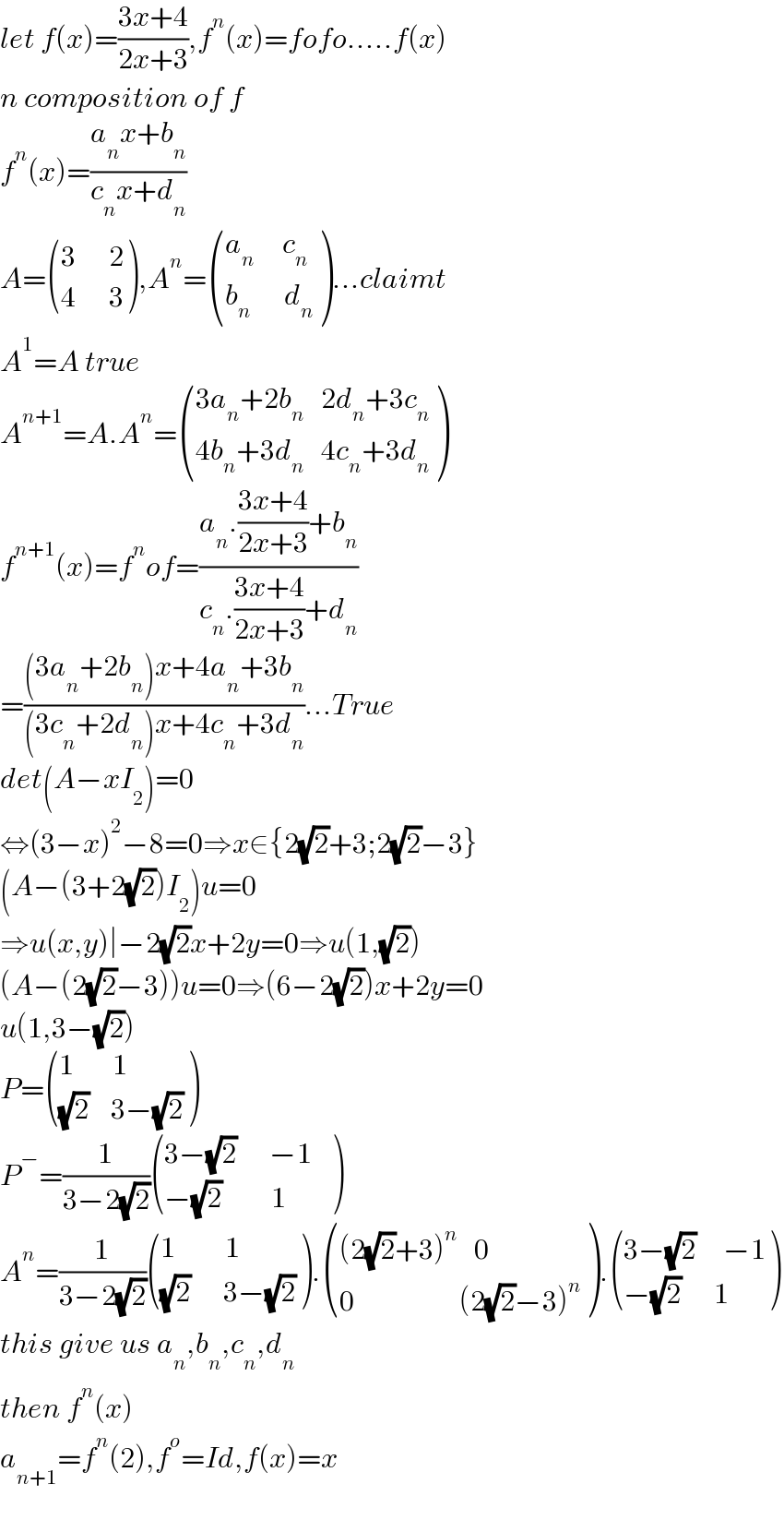
Commented by mr W last updated on 14/Jun/21
$${thanks}\:{sir}! \\ $$
Commented by mindispower last updated on 17/Jun/21
$${pleasur}\:{sir}\: \\ $$