Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 143462 by Willson last updated on 14/Jun/21

$$\underset{x\to 1}{\lim }\frac{x-1}{ln\left(\frac{x}{2-x}\right)}=???$$

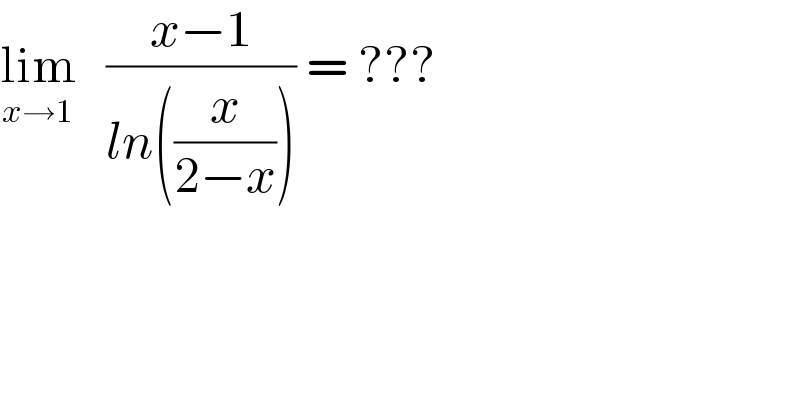
Answered by Dwaipayan Shikari last updated on 14/Jun/21

$$\underset{x\to 1}{\lim }\frac{x-1}{log\left(\frac{x}{2-x}\right)}=\underset{z\to 0}{\lim }\frac{z}{log\left(\frac{1+z}{1-z}\right)}=\frac{z}{2(z+\frac{z^3}{3}+..)}=\frac{1}{2}$$$$log\left(\frac{1+z}{1-z}\right)=z-\frac{z^2}{2}+\frac{z^3}{3}-..+(z+\frac{z^2}{2}+..)=2(z+\frac{z^3}{3}+..)$$

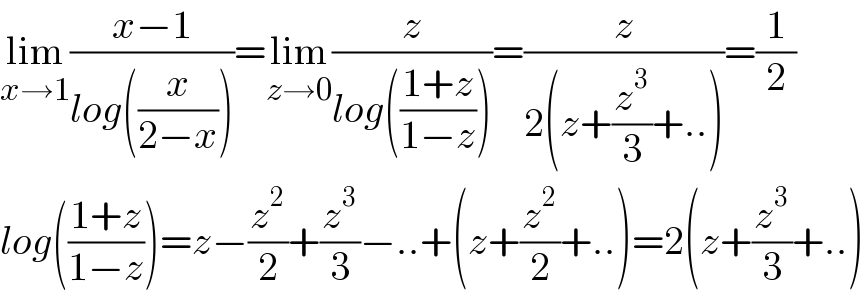
Answered by mnjuly1970 last updated on 14/Jun/21

$$solution:$$$$\mathrm{\Phi }:={lim}_{x\to 1}\frac{x-1}{ln\left(\frac{x}{2-x}\right)}\stackrel{⟨x-1=t⟩}{=}{lim}_{t\to 0}\left(\frac{t}{ln\left(\frac{t+1}{1-t}\right)}\right)$$$$:={lim}_{t\to 0}\left(\frac{t}{ln(1+t)-ln(1-t)}\right)$$$$:={lim}_{t\to 0}\left(\frac{t}{t-\frac{t^2}{2}+...-(-t-\frac{t^2}{2}...)}\right)$$$$:\approx {lim}_{t\to 0}\frac{t}{2t}=\frac{1}{2}.........\mathrm{\Phi }:=\frac{1}{2}$$

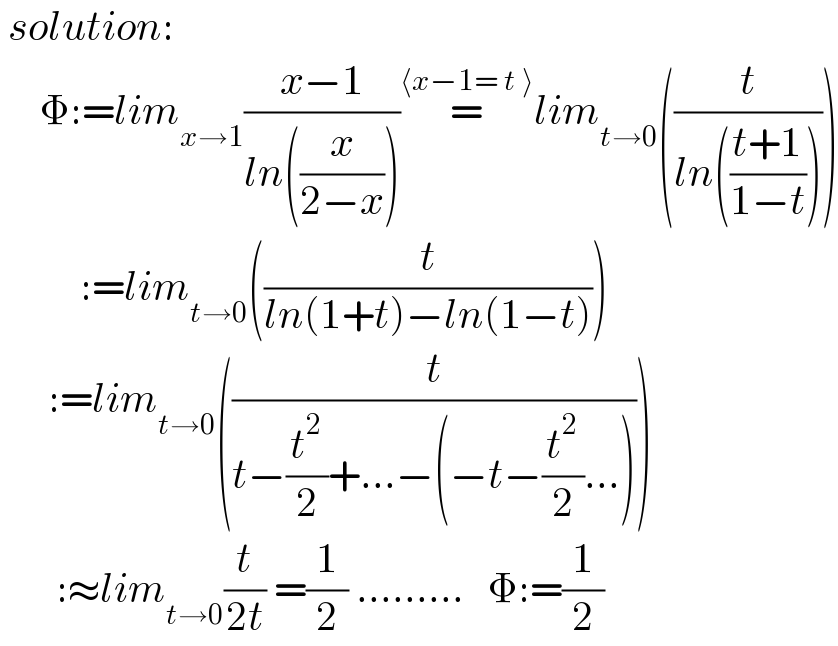
Answered by mathmax by abdo last updated on 14/Jun/21

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}-1}{\log \left(\frac{\mathrm{x}}{2-\mathrm{x}}\right)}\Rightarrow \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}-1}{\mathrm{logx}-\log (2-\mathrm{x})}$$$$\mathrm{changement}\mathrm{x}-1=\mathrm{t}\mathrm{give}\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{t}}{\log (1+\mathrm{t})-\log (2-\mathrm{t}-1)}=\mathrm{\Psi }\left(\mathrm{t}\right)(\mathrm{t}\to 0)$$$$=\frac{\mathrm{t}}{\log (1+\mathrm{t})-\log (1-\mathrm{t})}$$$${\log }^{{}^{\prime }}(1+\mathrm{t})=\frac{1}{1+\mathrm{t}}=1-\mathrm{t}+\mathrm{o}\left(\mathrm{t}\right)\Rightarrow \log (1+\mathrm{t})=\mathrm{t}-\frac{{\mathrm{t}}^2}{2}+\mathrm{o}\left({\mathrm{t}}^2\right)\mathrm{also}$$$$\log (1-\mathrm{t})=-\mathrm{t}-\frac{{\mathrm{t}}^2}{2}+\mathrm{o}\left({\mathrm{t}}^2\right)\Rightarrow$$$$\mathrm{\Psi }\left(\mathrm{t}\right)\sim \frac{\mathrm{t}}{\mathrm{t}-\frac{{\mathrm{t}}^2}{2}+\mathrm{t}+\frac{{\mathrm{t}}^2}{2}}=\frac{\mathrm{t}}{2\mathrm{t}}=\frac{1}{2}\Rightarrow {\lim }_{\mathrm{t}\to 0}\mathrm{\Psi }\left(\mathrm{t}\right)=\frac{1}{2}$$$$\Rightarrow {\lim }_{\mathrm{x}\to 1}\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{2}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com