
Question and Answers Forum
Question Number 143519 by tugu last updated on 15/Jun/21

Answered by mathmax by abdo last updated on 15/Jun/21
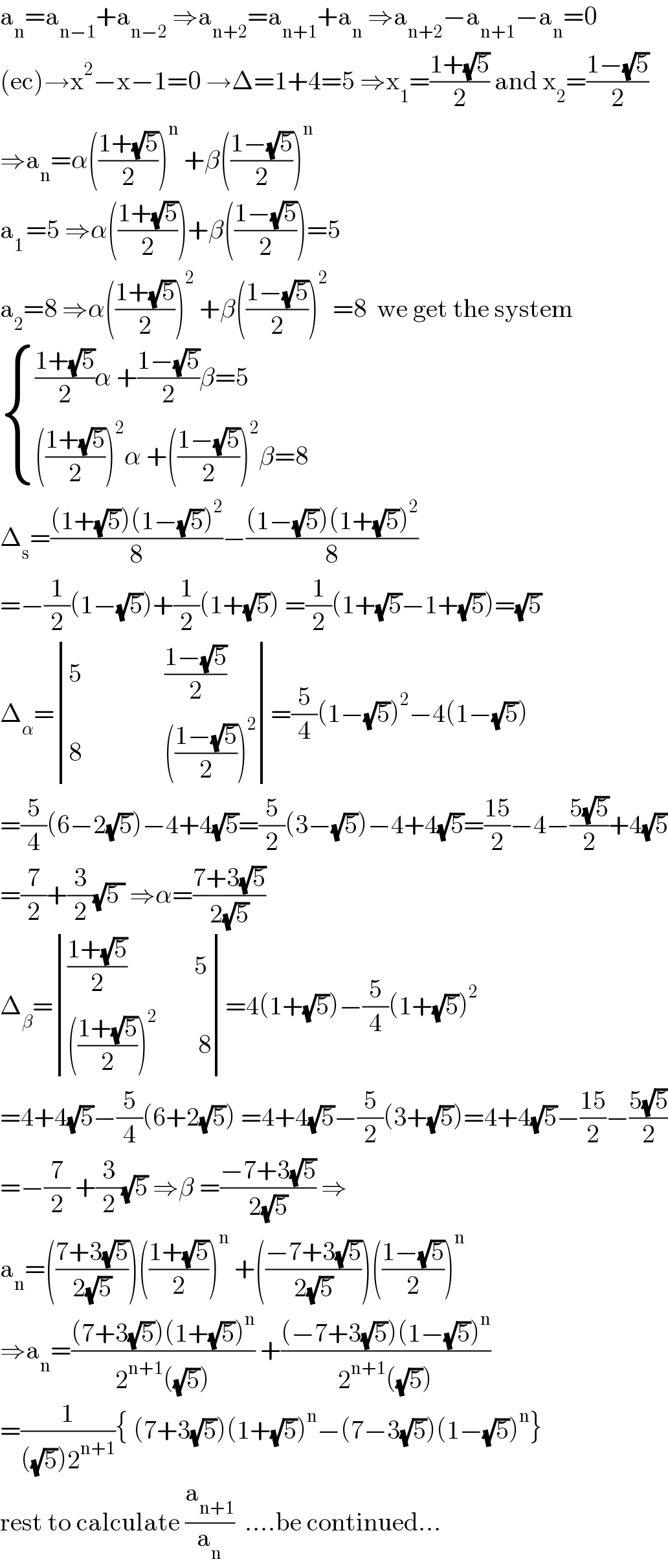
Answered by mr W last updated on 15/Jun/21
![x^2 −x−1=0 x=((1±(√5))/2) a_n =A(((1+(√5))/2))^n +B(((1−(√5))/2))^n a_0 =a_2 −a_1 =8−5=3=A+B ...(i) a_1 =5=A(((1+(√5))/2))+B(((1−(√5))/2)) ...(ii) ⇒A=((15+7(√5))/(10)) ⇒B=((15−7(√5))/(10)) a_n =(((15+7(√5))/(10)))(((1+(√5))/2))^n +(((15−7(√5))/(10)))(((1−(√5))/2))^n a_n =(((1+(√5))/2))^n [(((15+7(√5))/(10)))+(((15−7(√5))/(10)))(((1−(√5))/(1+(√5))))^n ] (a_(n+1) /a_n )=(((1+(√5))/2))×(((((15+7(√5))/(10)))+(((15−7(√5))/(10)))(((1−(√5))/(1+(√5))))^(n+1) )/((((15+7(√5))/(10)))+(((15−7(√5))/(10)))(((1−(√5))/(1+(√5))))^n )) lim_(n→∞) (a_(n+1) /a_n )=(((1+(√5))/2))×(((((15+7(√5))/(10)))+(((15−7(√5))/(10)))×0)/((((15+7(√5))/(10)))+(((15−7(√5))/(10)))×0))=((1+(√5))/2)=ϕ](Q143569.png)
Answered by mr W last updated on 15/Jun/21
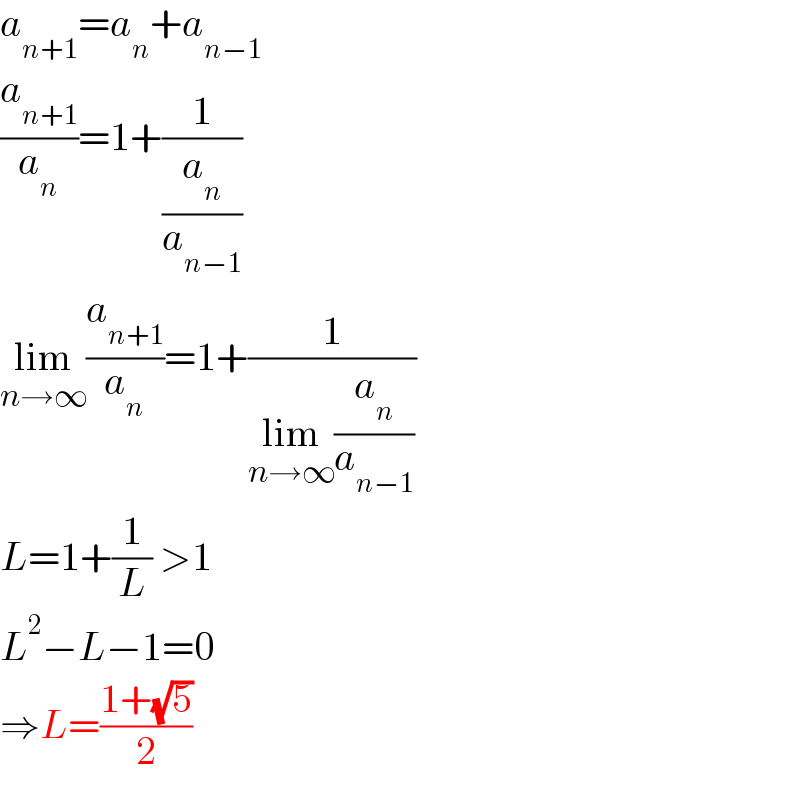
| ||
Question and Answers Forum | ||
Question Number 143519 by tugu last updated on 15/Jun/21 | ||
 | ||
Answered by mathmax by abdo last updated on 15/Jun/21 | ||
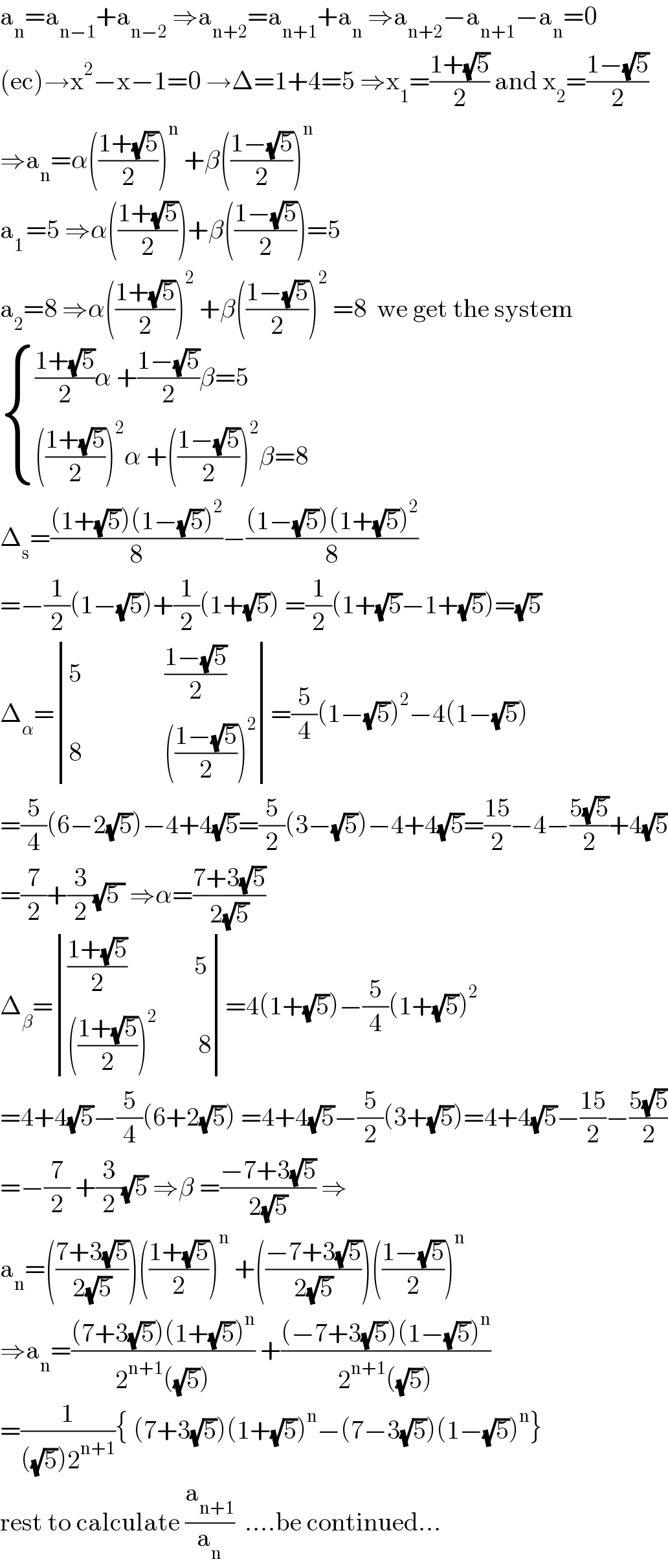 | ||
| ||
Answered by mr W last updated on 15/Jun/21 | ||
![x^2 −x−1=0 x=((1±(√5))/2) a_n =A(((1+(√5))/2))^n +B(((1−(√5))/2))^n a_0 =a_2 −a_1 =8−5=3=A+B ...(i) a_1 =5=A(((1+(√5))/2))+B(((1−(√5))/2)) ...(ii) ⇒A=((15+7(√5))/(10)) ⇒B=((15−7(√5))/(10)) a_n =(((15+7(√5))/(10)))(((1+(√5))/2))^n +(((15−7(√5))/(10)))(((1−(√5))/2))^n a_n =(((1+(√5))/2))^n [(((15+7(√5))/(10)))+(((15−7(√5))/(10)))(((1−(√5))/(1+(√5))))^n ] (a_(n+1) /a_n )=(((1+(√5))/2))×(((((15+7(√5))/(10)))+(((15−7(√5))/(10)))(((1−(√5))/(1+(√5))))^(n+1) )/((((15+7(√5))/(10)))+(((15−7(√5))/(10)))(((1−(√5))/(1+(√5))))^n )) lim_(n→∞) (a_(n+1) /a_n )=(((1+(√5))/2))×(((((15+7(√5))/(10)))+(((15−7(√5))/(10)))×0)/((((15+7(√5))/(10)))+(((15−7(√5))/(10)))×0))=((1+(√5))/2)=ϕ](Q143569.png) | ||
| ||
Answered by mr W last updated on 15/Jun/21 | ||
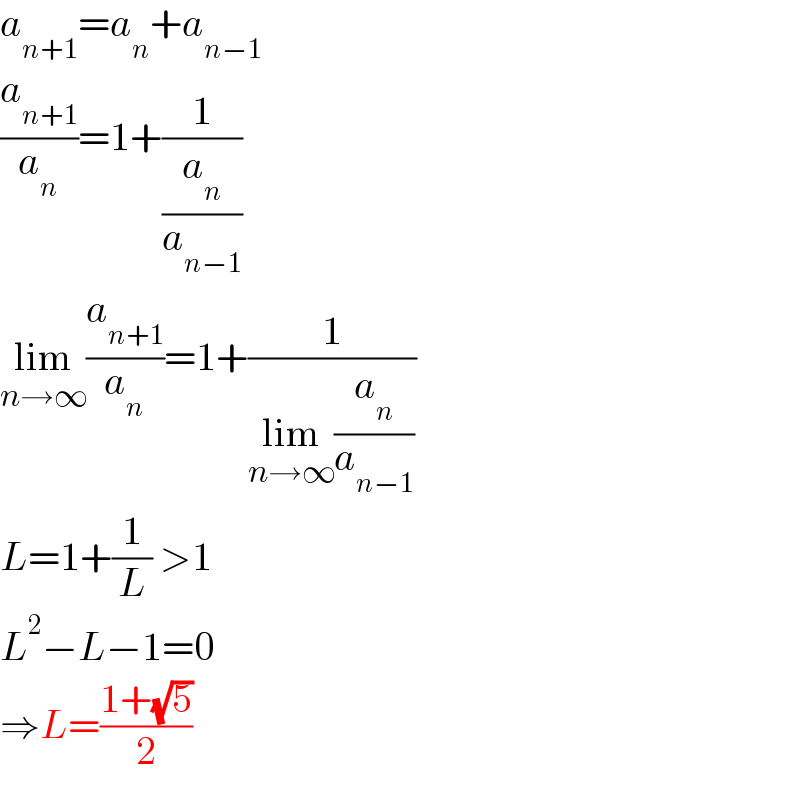 | ||
| ||