Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 14353 by tawa tawa last updated on 30/May/17

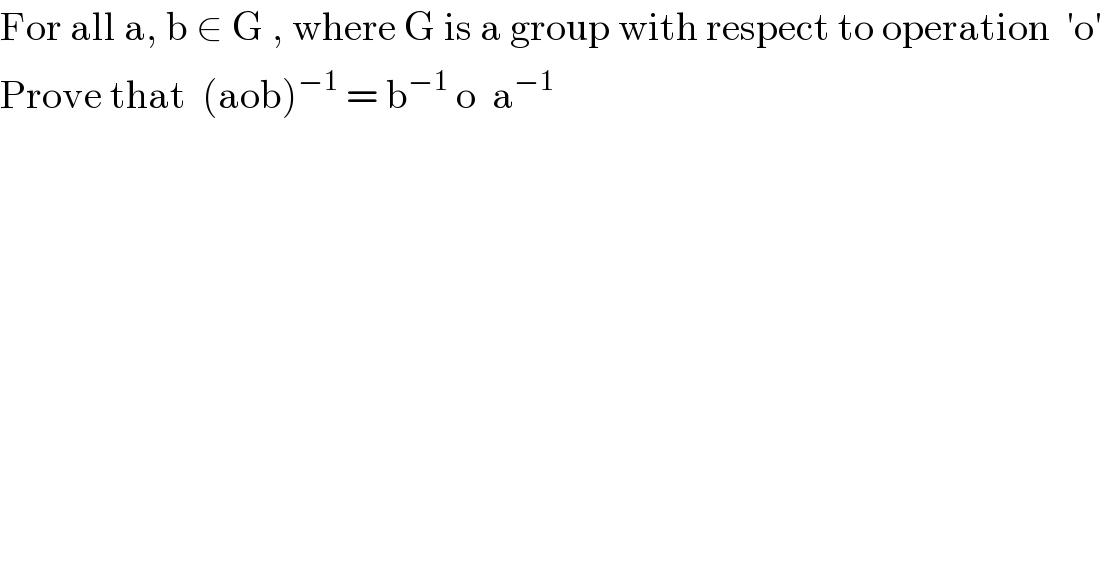
For all a, b ∈ G , where G is a group with respect to operation ′o′ Prove that (aob)^(−1) = b^(−1) o a^(−1)

$$\mathrm{For}\:\mathrm{all}\:\mathrm{a},\:\mathrm{b}\:\in\:\mathrm{G}\:,\:\mathrm{where}\:\mathrm{G}\:\mathrm{is}\:\mathrm{a}\:\mathrm{group}\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{operation}\:\:'\mathrm{o}' \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\:\left(\mathrm{aob}\right)^{−\mathrm{1}} \:=\:\mathrm{b}^{−\mathrm{1}} \:\mathrm{o}\:\:\mathrm{a}^{−\mathrm{1}} \\ $$

Commented by Tinkutara last updated on 31/May/17

Sorry, I want to say that are a and b functions on the set G? Also, is aob a composite function of b and a?

$$\mathrm{Sorry},\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{say}\:\mathrm{that}\:\mathrm{are}\:{a}\:\mathrm{and}\:{b} \\ $$$$\mathrm{functions}\:\mathrm{on}\:\mathrm{the}\:\mathrm{set}\:{G}? \\ $$$$\mathrm{Also},\:\mathrm{is}\:{aob}\:\mathrm{a}\:\mathrm{composite}\:\mathrm{function}\:\mathrm{of}\:{b} \\ $$$$\mathrm{and}\:{a}? \\ $$

Commented by tawa tawa last updated on 31/May/17

Yes sir

$$\mathrm{Yes}\:\mathrm{sir} \\ $$

Commented by Tinkutara last updated on 01/Jun/17

We have to show that (aob)o(b^(−1) oa^(−1) ) = I_G = (b^(−1) oa^(−1) )(aob) ⇒ (aob)o(b^(−1) oa^(−1) ) = ao(bob^(−1) )oa^(−1) = (aoI_G )oa^(−1) = aoa^(−1) = I_G Similarly you can prove the other part. [Here it is not needed to prove that aoa^(−1) = bob^(−1) = I_G , identity functions on G]

$$\mathrm{We}\:\mathrm{have}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\left({aob}\right){o}\left({b}^{−\mathrm{1}} {oa}^{−\mathrm{1}} \right) \\ $$$$=\:\mathrm{I}_{{G}} \:=\:\left({b}^{−\mathrm{1}} {oa}^{−\mathrm{1}} \right)\left({aob}\right) \\ $$$$\Rightarrow\:\left({aob}\right){o}\left({b}^{−\mathrm{1}} {oa}^{−\mathrm{1}} \right)\:=\:{ao}\left({bob}^{−\mathrm{1}} \right){oa}^{−\mathrm{1}} \\ $$$$=\:\left({ao}\mathrm{I}_{{G}} \right){oa}^{−\mathrm{1}} \:=\:{aoa}^{−\mathrm{1}} \:=\:\mathrm{I}_{{G}} \\ $$$$\mathrm{Similarly}\:\mathrm{you}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{other} \\ $$$$\mathrm{part}. \\ $$$$\left[\mathrm{Here}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{needed}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\right. \\ $$$${aoa}^{−\mathrm{1}} \:=\:{bob}^{−\mathrm{1}} \:=\:\mathrm{I}_{{G}} ,\:\mathrm{identity}\:\mathrm{functions} \\ $$$$\left.\mathrm{on}\:{G}\right] \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com