Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 143575 by Mathspace last updated on 15/Jun/21

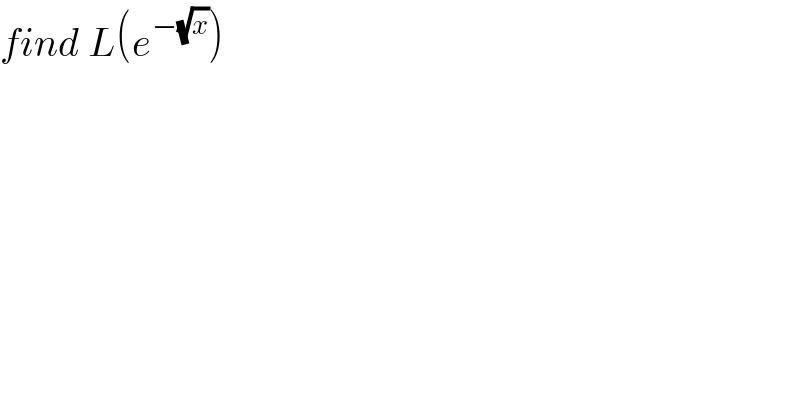
find L(e^(−(√x)) )

$${find}\:{L}\left({e}^{−\sqrt{{x}}} \right) \\ $$

Answered by Dwaipayan Shikari last updated on 15/Jun/21

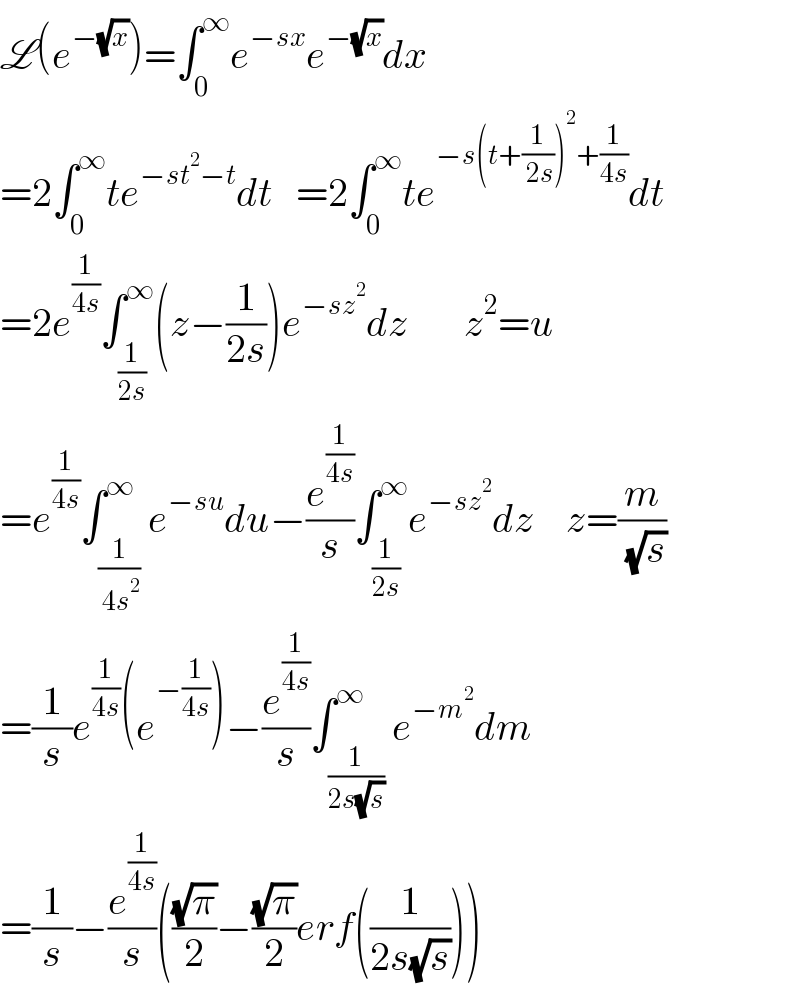
L(e^(−(√x)) )=∫_0 ^∞ e^(−sx) e^(−(√x)) dx =2∫_0 ^∞ te^(−st^2 −t) dt =2∫_0 ^∞ te^(−s(t+(1/( 2s)))^2 +(1/(4s))) dt =2e^(1/(4s)) ∫_(1/(2s)) ^∞ (z−(1/(2s)))e^(−sz^2 ) dz z^2 =u =e^(1/(4s)) ∫_(1/( 4s^2 )) ^∞ e^(−su) du−(e^(1/(4s)) /s)∫_(1/(2s)) ^∞ e^(−sz^2 ) dz z=(m/( (√s))) =(1/s)e^(1/(4s)) (e^(−(1/(4s))) )−(e^(1/(4s)) /s)∫_(1/(2s(√s))) ^∞ e^(−m^2 ) dm =(1/s)−(e^(1/(4s)) /s)(((√π)/2)−((√π)/2)erf((1/(2s(√s)))))

$$\mathscr{L}\left({e}^{−\sqrt{{x}}} \right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{sx}} {e}^{−\sqrt{{x}}} {dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {te}^{−{st}^{\mathrm{2}} −{t}} {dt}\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {te}^{−{s}\left({t}+\frac{\mathrm{1}}{\:\mathrm{2}{s}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}{s}}} {dt}\: \\ $$$$=\mathrm{2}{e}^{\frac{\mathrm{1}}{\mathrm{4}{s}}} \int_{\frac{\mathrm{1}}{\mathrm{2}{s}}} ^{\infty} \left({z}−\frac{\mathrm{1}}{\mathrm{2}{s}}\right){e}^{−{sz}^{\mathrm{2}} } {dz}\:\:\:\:\:\:\:{z}^{\mathrm{2}} ={u} \\ $$$$={e}^{\frac{\mathrm{1}}{\mathrm{4}{s}}} \int_{\frac{\mathrm{1}}{\:\mathrm{4}{s}^{\mathrm{2}} }} ^{\infty} {e}^{−{su}} {du}−\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}{s}}} }{{s}}\int_{\frac{\mathrm{1}}{\mathrm{2}{s}}} ^{\infty} {e}^{−{sz}^{\mathrm{2}} } {dz}\:\:\:\:{z}=\frac{{m}}{\:\sqrt{{s}}} \\ $$$$=\frac{\mathrm{1}}{{s}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{s}}} \left({e}^{−\frac{\mathrm{1}}{\mathrm{4}{s}}} \right)−\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}{s}}} }{{s}}\int_{\frac{\mathrm{1}}{\mathrm{2}{s}\sqrt{{s}}}} ^{\infty} {e}^{−{m}^{\mathrm{2}} } {dm} \\ $$$$=\frac{\mathrm{1}}{{s}}−\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}{s}}} }{{s}}\left(\frac{\sqrt{\pi}}{\mathrm{2}}−\frac{\sqrt{\pi}}{\mathrm{2}}{erf}\left(\frac{\mathrm{1}}{\mathrm{2}{s}\sqrt{{s}}}\right)\right) \\ $$

Commented by mathmax by abdo last updated on 16/Jun/21

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com