
Question and Answers Forum
Question Number 143588 by bobhans last updated on 16/Jun/21

Answered by EDWIN88 last updated on 16/Jun/21
![F(x)=∫_4 ^(8x) f(t) dt = (√(2+x^2 )) + c F ′(x)= 8f(8x)=(x/( (√(2+x^2 )))) F′(x)=f(8x)=(x/(8(√(2+x^2 )))) ⇒f(x)=(((1/8)x)/(8(√(2+(1/(64))x^2 )))) = (x/(8(√(128+x^2 )))) ⇒f(t)=(t/(8(√(128+t^2 )))) F(x)=∫_4 ^(8x) [(t/(8(√(128+t^2 )))) ]dt = (√(2+x^2 )) +c take x=(1/2) ⇒F((1/2))=∫_( 4) ^(8.(1/2)) [(t/(8(√(128+t^2 )))) ]dt =(√(2+(1/4))) +c ⇒ 0 = (3/2)+c ; c =−(3/2)](Q143590.png)
Answered by mathmax by abdo last updated on 16/Jun/21
![∫_4 ^(8x) f(t)dt=(√(2+x^2 )) +c by derivation we get 8f(8x)=((2x)/(2(√(2+x^2 ))))=(x/( (√(2+x^2 )))) ⇒f(8x)=(x/(8(√(2+x^2 )))) 8x=t ⇒f(t)=(t/(64(√(2+(t^2 /8^2 ))))) =(t/(8(√(128+t^2 )))) x=0 ⇒−∫_0 ^4 f(t)dt=(√2)+c ⇒c=−(√2)−∫_0 ^4 f(t)dt =−(√2)−(1/8)∫_0 ^4 (t/( (√(128+t^2 ))))dt =−(√2)[(√(128+t^2 ))]_0 ^4 =−(√2)((√(128+16))−(√(128)))=−(√2)((√(144))−(√(128)))](Q143619.png)
Answered by mindispower last updated on 16/Jun/21
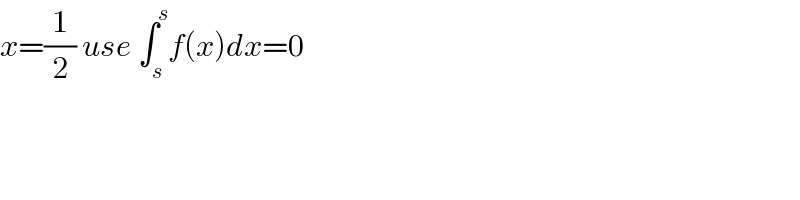
| ||
Question and Answers Forum | ||
Question Number 143588 by bobhans last updated on 16/Jun/21 | ||
 | ||
Answered by EDWIN88 last updated on 16/Jun/21 | ||
![F(x)=∫_4 ^(8x) f(t) dt = (√(2+x^2 )) + c F ′(x)= 8f(8x)=(x/( (√(2+x^2 )))) F′(x)=f(8x)=(x/(8(√(2+x^2 )))) ⇒f(x)=(((1/8)x)/(8(√(2+(1/(64))x^2 )))) = (x/(8(√(128+x^2 )))) ⇒f(t)=(t/(8(√(128+t^2 )))) F(x)=∫_4 ^(8x) [(t/(8(√(128+t^2 )))) ]dt = (√(2+x^2 )) +c take x=(1/2) ⇒F((1/2))=∫_( 4) ^(8.(1/2)) [(t/(8(√(128+t^2 )))) ]dt =(√(2+(1/4))) +c ⇒ 0 = (3/2)+c ; c =−(3/2)](Q143590.png) | ||
| ||
Answered by mathmax by abdo last updated on 16/Jun/21 | ||
![∫_4 ^(8x) f(t)dt=(√(2+x^2 )) +c by derivation we get 8f(8x)=((2x)/(2(√(2+x^2 ))))=(x/( (√(2+x^2 )))) ⇒f(8x)=(x/(8(√(2+x^2 )))) 8x=t ⇒f(t)=(t/(64(√(2+(t^2 /8^2 ))))) =(t/(8(√(128+t^2 )))) x=0 ⇒−∫_0 ^4 f(t)dt=(√2)+c ⇒c=−(√2)−∫_0 ^4 f(t)dt =−(√2)−(1/8)∫_0 ^4 (t/( (√(128+t^2 ))))dt =−(√2)[(√(128+t^2 ))]_0 ^4 =−(√2)((√(128+16))−(√(128)))=−(√2)((√(144))−(√(128)))](Q143619.png) | ||
| ||
Answered by mindispower last updated on 16/Jun/21 | ||
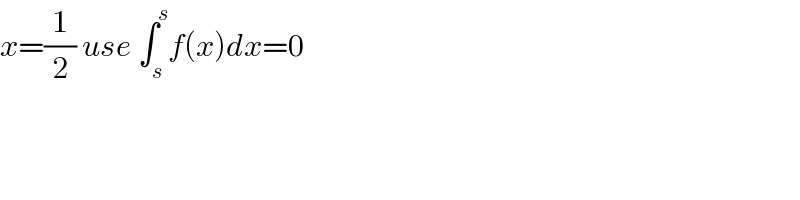 | ||
| ||