
Question and Answers Forum
Question Number 143609 by mnjuly1970 last updated on 16/Jun/21
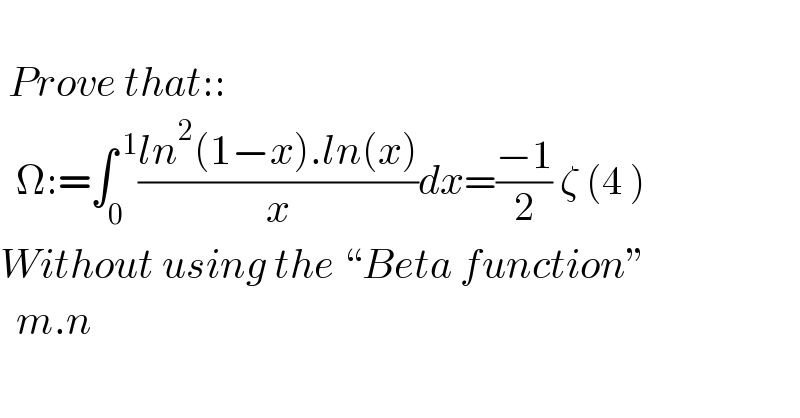
Answered by mindispower last updated on 16/Jun/21
![∫((ln(1−x))/x)dx=−li_2 (x) =−[li_2 (x)ln(x)ln(1−x)]_0 ^1 −∫_0 ^1 ((li_2 (x))/(1−x))ln(x)dx +∫_0 ^1 ((li_2 (x)ln(1−x))/x)dx =−∫_0 ^1 ((li_2 (x)ln(x))/(1−x))+∫_0 ^1 li_2 (x).(−d(li_2 (x)) =−∫_0 ^1 ((li_2 (x)ln(x))/(1−x))dx−(1/2)ζ^2 (2) −∫_0 ^1 ((li_2 (x)ln(x))/(1−x))dx=−Σ_(n≥1) Σ_(k≥0) ∫_0 ^1 (x^n /n^2 ).x^k ln(x)dx =Σ_(n≥1) Σ_(k≥0) (1/n^2 )∫_0 ^1 x^(n+k) (−ln(x))dx Σ_(n≥1) Σ_(k≥0) (1/(n^2 (n+k+1)))=Σ_(n≥1) Σ_(k≥n+1) (1/(k^2 n^2 ))=S start ζ(2).ζ(2)=Σ_(n≥1) Σ_(k≥1) (1/(n^2 k^2 ))=Σ_(n≥1) Σ_(k≥n+1) (1/(n^2 k^2 ))+Σ_(n≥1) (1/(n^2 .n^2 )) +Σ_(n≥2 ) Σ_(k≤n−1) (1/(n^2 k^2 )) ⇒2Σ_(n≥1) Σ_(k≥n+1) (1/(n^2 k^2 ))+ζ(4)=ζ^2 (2) ⇒S=−((ζ(4))/2)+((ζ^2 (2))/2) Ω=−((ζ(4))/2)+((ζ^2 (2))/2)−((ζ^2 (2))/2)=((ζ(4))/2)](Q143656.png)
| ||
Question and Answers Forum | ||
Question Number 143609 by mnjuly1970 last updated on 16/Jun/21 | ||
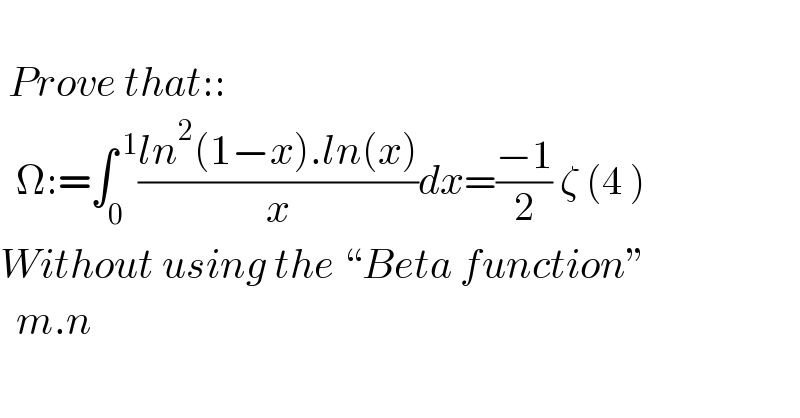 | ||
Answered by mindispower last updated on 16/Jun/21 | ||
![∫((ln(1−x))/x)dx=−li_2 (x) =−[li_2 (x)ln(x)ln(1−x)]_0 ^1 −∫_0 ^1 ((li_2 (x))/(1−x))ln(x)dx +∫_0 ^1 ((li_2 (x)ln(1−x))/x)dx =−∫_0 ^1 ((li_2 (x)ln(x))/(1−x))+∫_0 ^1 li_2 (x).(−d(li_2 (x)) =−∫_0 ^1 ((li_2 (x)ln(x))/(1−x))dx−(1/2)ζ^2 (2) −∫_0 ^1 ((li_2 (x)ln(x))/(1−x))dx=−Σ_(n≥1) Σ_(k≥0) ∫_0 ^1 (x^n /n^2 ).x^k ln(x)dx =Σ_(n≥1) Σ_(k≥0) (1/n^2 )∫_0 ^1 x^(n+k) (−ln(x))dx Σ_(n≥1) Σ_(k≥0) (1/(n^2 (n+k+1)))=Σ_(n≥1) Σ_(k≥n+1) (1/(k^2 n^2 ))=S start ζ(2).ζ(2)=Σ_(n≥1) Σ_(k≥1) (1/(n^2 k^2 ))=Σ_(n≥1) Σ_(k≥n+1) (1/(n^2 k^2 ))+Σ_(n≥1) (1/(n^2 .n^2 )) +Σ_(n≥2 ) Σ_(k≤n−1) (1/(n^2 k^2 )) ⇒2Σ_(n≥1) Σ_(k≥n+1) (1/(n^2 k^2 ))+ζ(4)=ζ^2 (2) ⇒S=−((ζ(4))/2)+((ζ^2 (2))/2) Ω=−((ζ(4))/2)+((ζ^2 (2))/2)−((ζ^2 (2))/2)=((ζ(4))/2)](Q143656.png) | ||
| ||