
Question and Answers Forum
Question Number 143684 by Huy last updated on 17/Jun/21
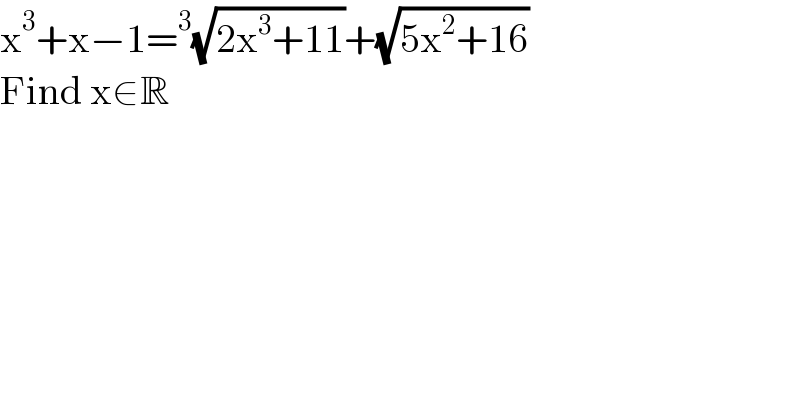
Answered by TheHoneyCat last updated on 17/Jun/21
![let x_0 =2 x_0 is a solution (2^3 +2−1=9=^3 (√(27))+(√(36))) Juging by the graph, it seems it is the only solution let me proove it let x∈]x_0 ,+∞[ let f: x→x^3 +x−1 and g: x→^3 (√(2x^3 +11))+(√(5x^2 +16)) (df/dx)=3x^2 +1 (dg/dx)=6x^2 (2x^3 +11)^(−(2/3)) +10x(5x^2 +16)^(−(1/2)) x≥2 ⇒2x^3 ≥16 ⇒2x^3 +11≥27 ⇒(2x^3 +11)^(1/3) ≥3 ⇒(2x^3 +11)^(2/3) ≥9 ⇒(2x^3 +11)^((−2)/3) ≤(1/9) ⇒6x^2 (2x^3 +11)^((−2)/3) ≤(2/9)3x^2 5x^2 +16≥5x^2 ⇒(5x^2 +16)^(1/2) ≥(√5)x ⇒10x(5x^2 +16)^((−1)/2) ≤((10)/( (√5))) and 3x^2 +1≥(2/9)3x^2 +((10)/( (√5))) so (df/dx)≥(dg/dx) so ∀x≥x_0 f(x)≠g(x) the same reasonning can be donne for x∈[0,x_0 ] and for x<0 checking the sine is sufficient_■](Q143695.png)
Commented by TheHoneyCat last updated on 17/Jun/21

| ||
Question and Answers Forum | ||
Question Number 143684 by Huy last updated on 17/Jun/21 | ||
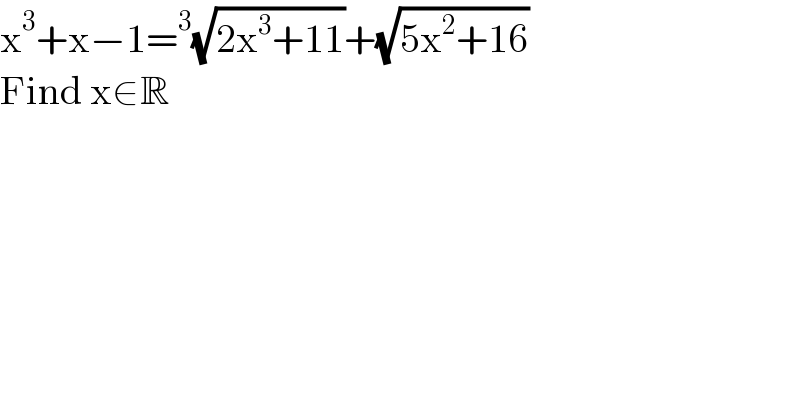 | ||
Answered by TheHoneyCat last updated on 17/Jun/21 | ||
![let x_0 =2 x_0 is a solution (2^3 +2−1=9=^3 (√(27))+(√(36))) Juging by the graph, it seems it is the only solution let me proove it let x∈]x_0 ,+∞[ let f: x→x^3 +x−1 and g: x→^3 (√(2x^3 +11))+(√(5x^2 +16)) (df/dx)=3x^2 +1 (dg/dx)=6x^2 (2x^3 +11)^(−(2/3)) +10x(5x^2 +16)^(−(1/2)) x≥2 ⇒2x^3 ≥16 ⇒2x^3 +11≥27 ⇒(2x^3 +11)^(1/3) ≥3 ⇒(2x^3 +11)^(2/3) ≥9 ⇒(2x^3 +11)^((−2)/3) ≤(1/9) ⇒6x^2 (2x^3 +11)^((−2)/3) ≤(2/9)3x^2 5x^2 +16≥5x^2 ⇒(5x^2 +16)^(1/2) ≥(√5)x ⇒10x(5x^2 +16)^((−1)/2) ≤((10)/( (√5))) and 3x^2 +1≥(2/9)3x^2 +((10)/( (√5))) so (df/dx)≥(dg/dx) so ∀x≥x_0 f(x)≠g(x) the same reasonning can be donne for x∈[0,x_0 ] and for x<0 checking the sine is sufficient_■](Q143695.png) | ||
| ||
Commented by TheHoneyCat last updated on 17/Jun/21 | ||
 | ||