
Question and Answers Forum
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 143740 by Willson last updated on 17/Jun/21
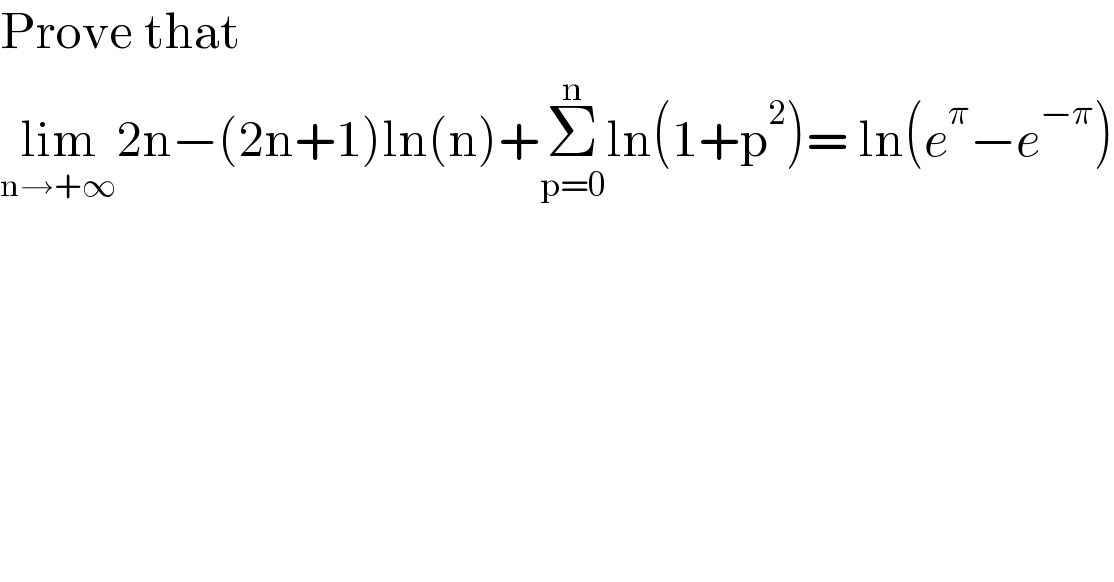
Answered by TheHoneyCat last updated on 17/Jun/21

| ||
Question and Answers Forum | ||
Previous in Permutation and Combination Next in Permutation and Combination | ||
Question Number 143740 by Willson last updated on 17/Jun/21 | ||
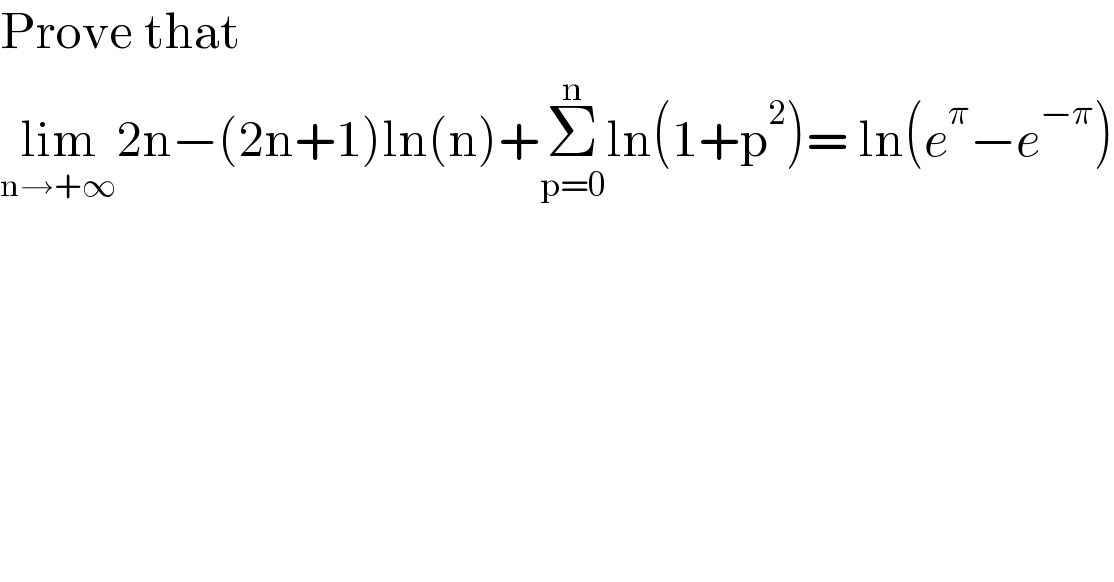 | ||
Answered by TheHoneyCat last updated on 17/Jun/21 | ||
 | ||
| ||