Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 143878 by akmalovna05 last updated on 19/Jun/21

$${\mathrm{y}}^{‴}={2\mathrm{xy}}^{″}$$

Answered by Ar Brandon last updated on 19/Jun/21

$${\mathrm{y}}^{‴}={2\mathrm{xy}}^{″}\Rightarrow \frac{{\mathrm{y}}^{‴}}{{\mathrm{y}}^{″}}=2\mathrm{x}\Rightarrow \ln \left({\mathrm{y}}^{″}\right)={\mathrm{x}}^2\Rightarrow {\mathrm{y}}^{″}={\mathrm{e}}^{{\mathrm{x}}^2}$$

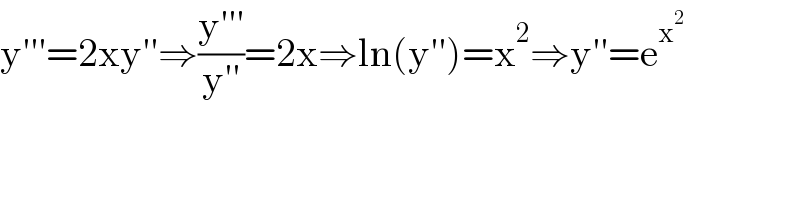
Answered by ajfour last updated on 19/Jun/21

$$d\left(\frac{d^{2}y}{{dx}^2}\right)=2x\left(\frac{d^{2}y}{{dx}^2}\right)dx$$$$\Rightarrow \ln \left(\frac{d^{2}y}{{dx}^2}\right)=x^2+c$$$$d\left(\frac{dy}{dx}\right)={ke}^{x^2}$$$$\frac{dy}{dx}=(k\int e^{x^2}dx)+b$$$$y=\int (k\int e^{x^2}dx)dx+bx+a$$

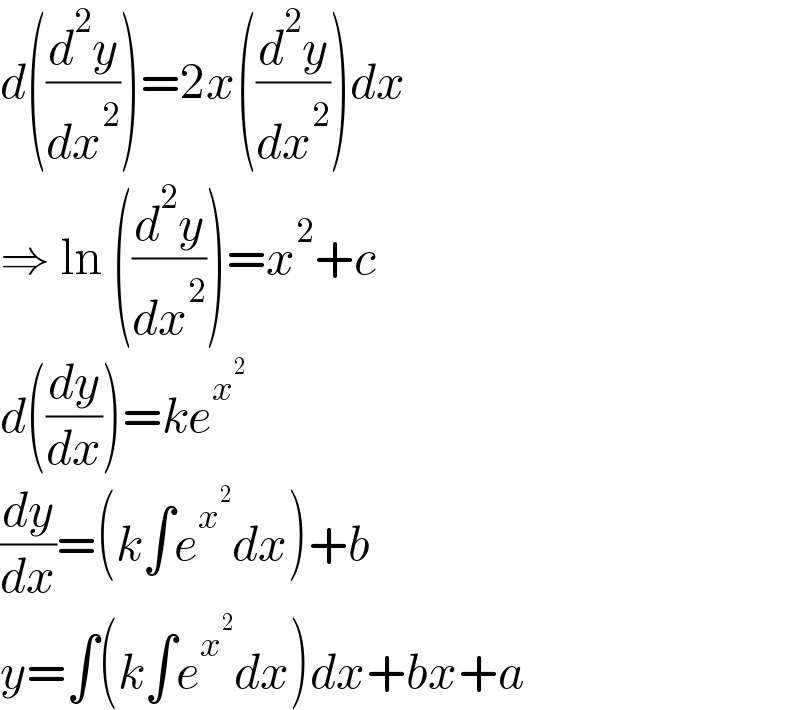
Answered by Olaf_Thorendsen last updated on 19/Jun/21

$$y^{‴}=2{xy}^{″}$$$$\frac{y^{‴}}{y^{″}}=2x$$$$\ln \mid y^{″}\mid =x^2+{\mathrm{C}}_1$$$$y^{″}={\mathrm{C}}_2{e}^{x^2}$$$$y^{\prime }=\int {\mathrm{C}}_2{e}^{x^2}dx={\mathrm{C}}_2\left(\frac{\sqrt{\pi }}{2}\mathrm{erfi}\left(x\right)\right)+{\mathrm{C}}_3$$$$y^{\prime }={\mathrm{C}}_4\mathrm{erfi}\left(x\right)+{\mathrm{C}}_3$$$$\mathrm{erfi}\left(x\right)=\frac{2}{\sqrt{\pi }}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{(2n+1)n!}{x}^{2n+1}$$$$y^{\prime }={\mathrm{C}}_5\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{(2n+1)n!}{x}^{2n+1}+{\mathrm{C}}_3$$$$y={\mathrm{C}}_5\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{(2n+1)(2n+2)n!}{x}^{2n+2}+{\mathrm{C}}_{3}x+{\mathrm{C}}_6$$$$y=\frac{{\mathrm{C}}_5}{2}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{(n+1)(2n+1)n!}{x}^{2n+2}+{\mathrm{C}}_{3}x+{\mathrm{C}}_6$$$$\mathrm{Finally}:$$$$y=a\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{(n+1)(2n+1)n!}{x}^{2n+2}+bx+c$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com