Question Number 143889 by mnjuly1970 last updated on 19/Jun/21
$$ \\ $$$$\:\:\:\:\:\:{A}\:\:{Challanging}\:\:{Integral}: \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{log}\left({x}\right).{log}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}{dx} \\ $$$$ \\ $$$$ \\ $$
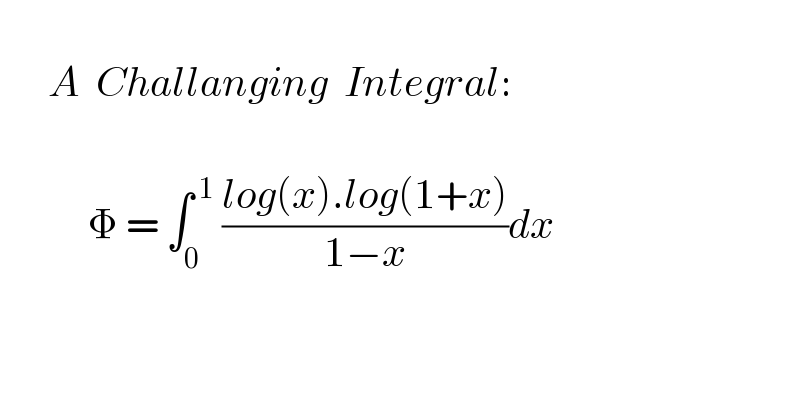
Answered by Olaf_Thorendsen last updated on 19/Jun/21
![Φ = ∫_0 ^1 ((ln(x).ln(1+x))/(1−x)) dx Let u = 1−x Φ = ∫_0 ^1 ((ln(1−u).ln(2−u))/u) du Φ = ∫_0 ^1 ((ln(2−u))/u)(−Σ_(n=0) ^∞ (u^(n+1) /(n+1))) du Φ = −∫_0 ^1 ln(2−u)Σ_(n=0) ^∞ (u^n /(n+1)) du Φ = −[ln(2−u)Σ_(n=0) ^∞ (u^(n+1) /((n+1)^2 ))]_0 ^1 −∫_0 ^1 (1/(2−u)).Σ_(n=0) ^∞ (u^(n+1) /((n+1)^2 )) du Φ = Σ_(n=0() ^∞ (1/(n+1)^2 ))∫_0 ^1 (u^(n+1) /(2−u)) du Let I_n = ∫_0 ^1 (u^n /(2−u)) du 2I_n −I_(n+1) = ∫_0 ^1 ((2u^n −u^(n+1) )/(2−u)) du 2I_n −I_(n+1) = ∫_0 ^1 u^n du 2I_n −I_(n+1) = (1/(n+1)) I_(n+1) = 2I_n −(1/(n+1)) I_(n+1) = 2(2I_(n−1) −(1/n))−(1/(n+1)) I_(n+1) = 2^2 I_(n−1) −(2/n)−(1/(n+1)) I_(n+1) = 2^2 I_(n−1) −(2/n)−(1/(n+1)) I_(n+1) = 2^3 I_(n−2) −(2^2 /(n−1))−(2/n)−(1/(n+1)) ... I_(n+1) = 2^(n+1) I_0 −Σ_(k=1) ^(n+1) (2^(n+1−k) /k) I_0 = ∫_0 ^1 (u^0 /(2−u)) du = [−ln∣2−u∣]_0 ^1 = ln2 I_(n+1) = 2^(n+1) ln2−Σ_(k=1) ^(n+1) (2^(n+1−k) /k) Φ = Σ_(n=0() ^∞ (I_(n+1) /(n+1)^2 )) Φ = Σ_(n=0() ^∞ (1/(n+1)^2 ))(2^(n+1) ln2−Σ_(k=1) ^(n+1) (2^(n+1−k) /k)) Φ = Σ_(n=0() ^∞ (2^(n+1) /(n+1)^2 ))(ln2−Σ_(k=1) ^(n+1) (2^(−k) /k)) Σ_(k=1) ^n (1/(2^k k)) = ln2−((n−1)/n).((LerchPhi((1/2),1,n))/2^(n+1) ) Φ = (1/2)Σ_(n=0) ^∞ (n.((LerchPhi((1/2),1,n+1))/((n+1)^3 ))) ... Sorry, I tried to solve but I′m lost...](Q143943.png)
$$ \\ $$$$\Phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right).\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{1}−{x} \\ $$$$\Phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−{u}\right).\mathrm{ln}\left(\mathrm{2}−{u}\right)}{{u}}\:{du} \\ $$$$\Phi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{2}−{u}\right)}{{u}}\left(−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\right)\:{du} \\ $$$$\Phi\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{2}−{u}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{n}} }{{n}+\mathrm{1}}\:{du} \\ $$$$\Phi\:=\:−\left[\mathrm{ln}\left(\mathrm{2}−{u}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}−{u}}.\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:{du} \\ $$$$\Phi\:=\:\underset{{n}=\mathrm{0}\left(\right.} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left.{n}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{{n}+\mathrm{1}} }{\mathrm{2}−{u}}\:{du} \\ $$$$\mathrm{Let}\:\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{{n}} }{\mathrm{2}−{u}}\:{du} \\ $$$$\mathrm{2I}_{{n}} −\mathrm{I}_{{n}+\mathrm{1}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{u}^{{n}} −{u}^{{n}+\mathrm{1}} }{\mathrm{2}−{u}}\:{du} \\ $$$$\mathrm{2I}_{{n}} −\mathrm{I}_{{n}+\mathrm{1}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{{n}} \:{du} \\ $$$$\mathrm{2I}_{{n}} −\mathrm{I}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2I}_{{n}} −\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}\left(\mathrm{2I}_{{n}−\mathrm{1}} −\frac{\mathrm{1}}{{n}}\right)−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{\mathrm{2}} \mathrm{I}_{{n}−\mathrm{1}} −\frac{\mathrm{2}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{\mathrm{2}} \mathrm{I}_{{n}−\mathrm{1}} −\frac{\mathrm{2}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{\mathrm{3}} \mathrm{I}_{{n}−\mathrm{2}} −\frac{\mathrm{2}^{\mathrm{2}} }{{n}−\mathrm{1}}−\frac{\mathrm{2}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$... \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{{n}+\mathrm{1}} \mathrm{I}_{\mathrm{0}} −\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\mathrm{2}^{{n}+\mathrm{1}−{k}} }{{k}} \\ $$$$\mathrm{I}_{\mathrm{0}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{0}} }{\mathrm{2}−{u}}\:{du}\:=\:\left[−\mathrm{ln}\mid\mathrm{2}−{u}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\mathrm{ln2} \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{{n}+\mathrm{1}} \mathrm{ln2}−\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\mathrm{2}^{{n}+\mathrm{1}−{k}} }{{k}} \\ $$$$\Phi\:=\:\underset{{n}=\mathrm{0}\left(\right.} {\overset{\infty} {\sum}}\frac{\mathrm{I}_{{n}+\mathrm{1}} }{\left.{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Phi\:=\:\underset{{n}=\mathrm{0}\left(\right.} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left.{n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{2}^{{n}+\mathrm{1}} \mathrm{ln2}−\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\mathrm{2}^{{n}+\mathrm{1}−{k}} }{{k}}\right) \\ $$$$\Phi\:=\:\underset{{n}=\mathrm{0}\left(\right.} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}+\mathrm{1}} }{\left.{n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{ln2}−\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\mathrm{2}^{−{k}} }{{k}}\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} {k}}\:=\:\mathrm{ln2}−\frac{{n}−\mathrm{1}}{{n}}.\frac{\mathrm{LerchPhi}\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1},{n}\right)}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}.\frac{\mathrm{LerchPhi}\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1},{n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }\right) \\ $$$$... \\ $$$$\mathrm{Sorry},\:\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{lost}... \\ $$
Commented by mnjuly1970 last updated on 20/Jun/21
$$\:{thanks}\:{alot}\:{mr}\:{olaf}\:.. \\ $$
Answered by mnjuly1970 last updated on 20/Jun/21
$$\:\:\:\:\Phi:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}\right){log}\left(\mathrm{2}−{x}\right)}{{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}\right)\left\{{log}\left(\mathrm{2}\right)+{log}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\right\}}{{x}}{dx} \\ $$$$\:\:\::=−{log}\left(\mathrm{2}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}−\mathrm{1}} {log}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\::=−{log}\left(\mathrm{2}\right).\frac{\pi^{\mathrm{2}} }{\mathrm{2}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{H}_{{n}} }{{n}^{\mathrm{2}} \mathrm{2}^{{n}} } \\ $$$$\:\:\::=−{log}\left(\mathrm{2}\right).\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}}\:+\zeta\left(\mathrm{3}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:{log}\left(\mathrm{2}\right) \\ $$$$\:\::=\frac{−\pi^{\:\mathrm{2}} }{\mathrm{4}}{log}\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)\:... \\ $$$$\: \\ $$
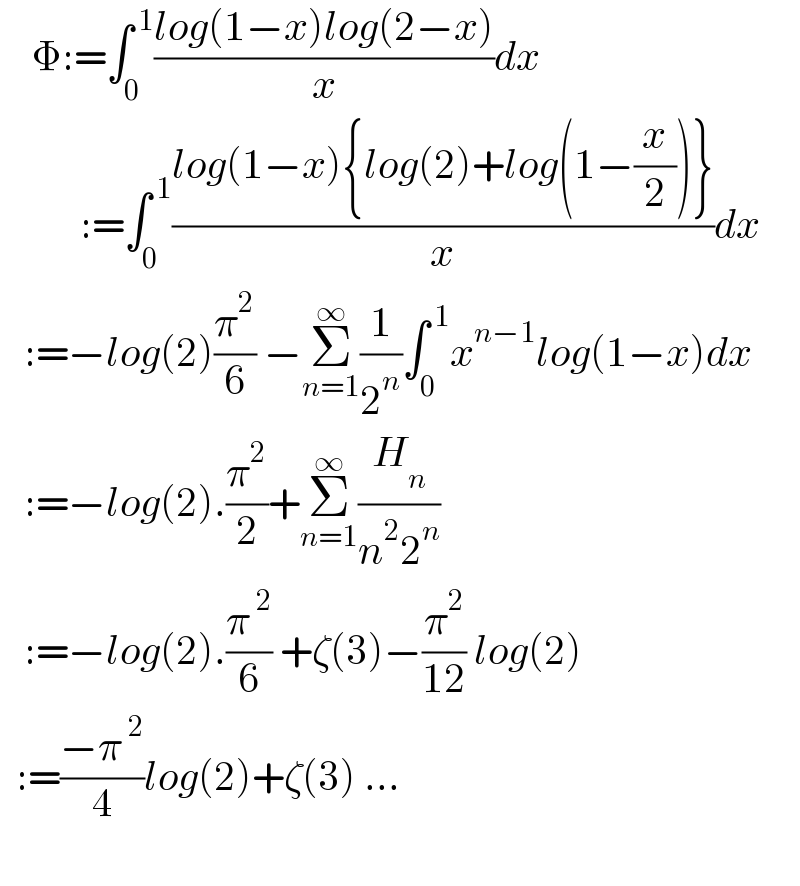
Commented by Dwaipayan Shikari last updated on 20/Jun/21
$${Nice}\:{sir}! \\ $$
Commented by mnjuly1970 last updated on 20/Jun/21
$$\:\:{thank}\:{you}\:{so}\:{much}... \\ $$