
Question and Answers Forum
Question Number 143964 by naka3546 last updated on 20/Jun/21
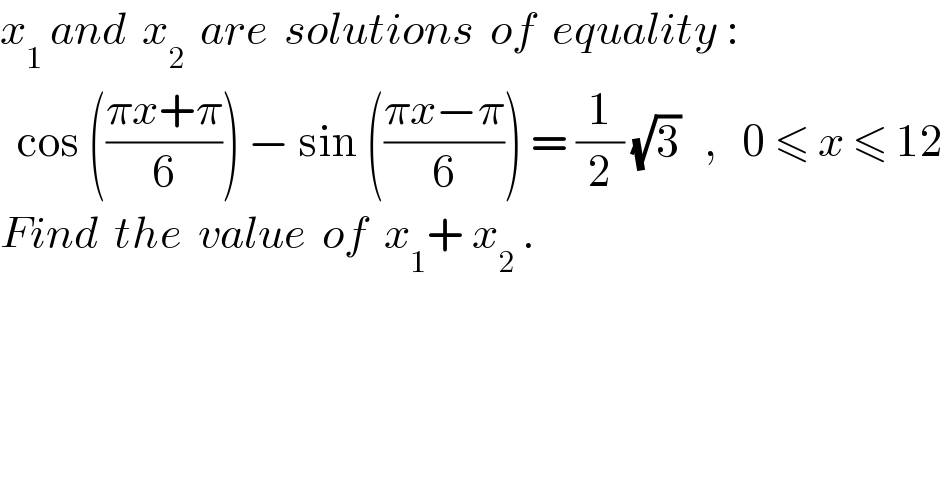
Commented by Canebulok last updated on 20/Jun/21
![Solution: By squaring both sides, ⇒ cos(((πx)/6) + (π/6))−sin(((πx)/(6 )) − (π/6)) = ((√3)/2) ⇒ [cos(((πx)/6))cos((π/6))−sin(((πx)/6))sin((π/6))] − [sin(((πx)/6))cos((π/6))−cos(((πx)/6))sin((π/6))] = ((√3)/2)](Q143975.png)
Commented by Canebulok last updated on 20/Jun/21
![Solution: ⇒ [cos(((πx)/6))cos((π/6))−sin(((πx)/6))cos((π/6))] + [cos(((πx)/6))sin((π/6))−sin(((πx)/6))sin((π/6))] = ((√3)/2) ⇒ cos((π/6))[cos(((πx)/6))−sin(((πx)/6))] + sin((π/6))[cos(((πx)/6))−sin(((πx)/6))] = ((√3)/2) ⇒ [cos((π/6))+sin((π/6))][cos(((πx)/6))−sin(((πx)/6))] = ((√3)/2) By squaring both sides, ⇒ [1+2cos((π/6))sin((π/6))][1−2sin(((πx)/6))cos(((πx)/6))] = (3/4) ⇒ [1+sin((π/3))][1−sin(((πx)/3))] = (3/4) ⇒ 1−sin(((πx)/3)) = (3/(4[1+sin((π/3))])) ⇒ −sin(((πx)/3)) = (3/((4+4sin((π/3))))) − 1 ⇒ sin(((πx)/3)) = 1 − (3/((4+4sin((π/3))))) ⇒ arcsin[1−(3/((4+4sin((π/3)))))] = ((πx)/3) ⇒ arcsin[1−(3/((4+4sin((π/3)))))] ((3/π)) = x ∼ Kevin](Q143981.png)
Answered by bramlexs22 last updated on 20/Jun/21
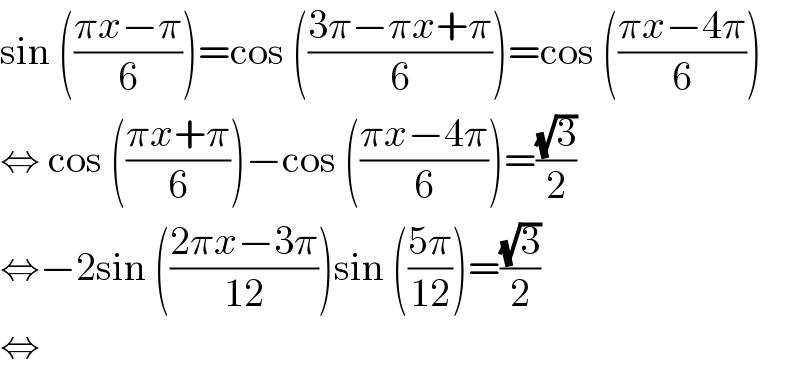
| ||
Question and Answers Forum | ||
Question Number 143964 by naka3546 last updated on 20/Jun/21 | ||
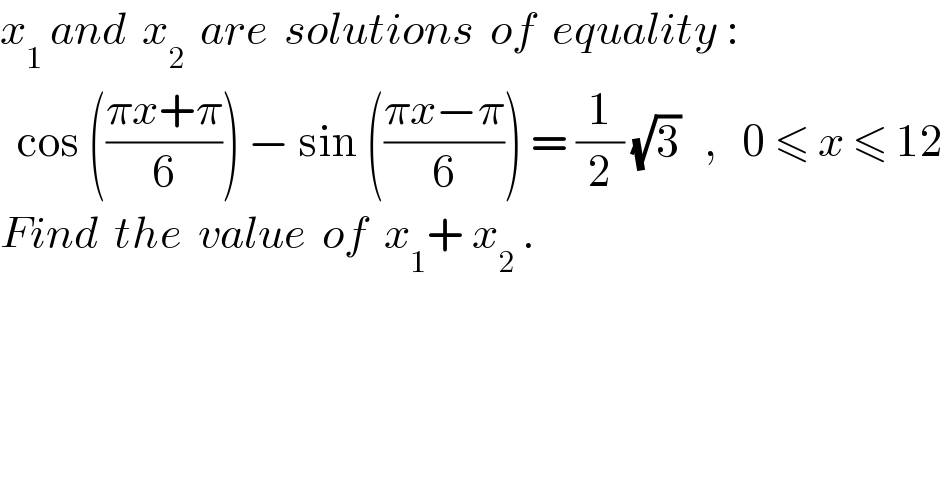 | ||
Commented by Canebulok last updated on 20/Jun/21 | ||
![Solution: By squaring both sides, ⇒ cos(((πx)/6) + (π/6))−sin(((πx)/(6 )) − (π/6)) = ((√3)/2) ⇒ [cos(((πx)/6))cos((π/6))−sin(((πx)/6))sin((π/6))] − [sin(((πx)/6))cos((π/6))−cos(((πx)/6))sin((π/6))] = ((√3)/2)](Q143975.png) | ||
Commented by Canebulok last updated on 20/Jun/21 | ||
![Solution: ⇒ [cos(((πx)/6))cos((π/6))−sin(((πx)/6))cos((π/6))] + [cos(((πx)/6))sin((π/6))−sin(((πx)/6))sin((π/6))] = ((√3)/2) ⇒ cos((π/6))[cos(((πx)/6))−sin(((πx)/6))] + sin((π/6))[cos(((πx)/6))−sin(((πx)/6))] = ((√3)/2) ⇒ [cos((π/6))+sin((π/6))][cos(((πx)/6))−sin(((πx)/6))] = ((√3)/2) By squaring both sides, ⇒ [1+2cos((π/6))sin((π/6))][1−2sin(((πx)/6))cos(((πx)/6))] = (3/4) ⇒ [1+sin((π/3))][1−sin(((πx)/3))] = (3/4) ⇒ 1−sin(((πx)/3)) = (3/(4[1+sin((π/3))])) ⇒ −sin(((πx)/3)) = (3/((4+4sin((π/3))))) − 1 ⇒ sin(((πx)/3)) = 1 − (3/((4+4sin((π/3))))) ⇒ arcsin[1−(3/((4+4sin((π/3)))))] = ((πx)/3) ⇒ arcsin[1−(3/((4+4sin((π/3)))))] ((3/π)) = x ∼ Kevin](Q143981.png) | ||
Answered by bramlexs22 last updated on 20/Jun/21 | ||
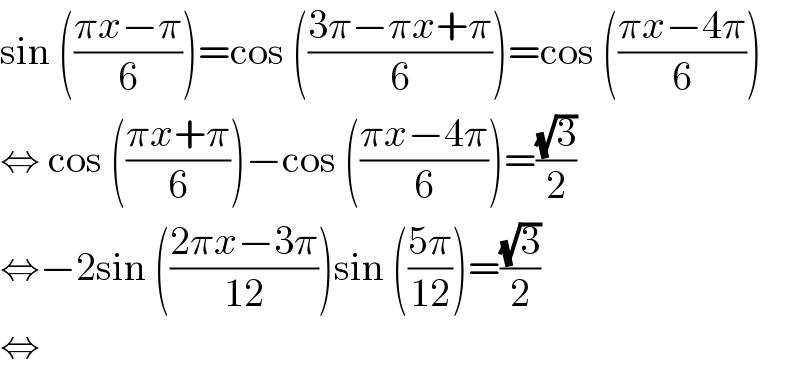 | ||
| ||