
Question and Answers Forum
Question Number 144026 by mohammad17 last updated on 20/Jun/21
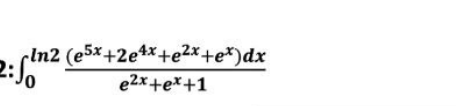
Commented by mohammad17 last updated on 20/Jun/21

Answered by Olaf_Thorendsen last updated on 20/Jun/21
![Ω = ∫_0 ^(ln2) ((e^(5x) +2e^(4x) +e^(2x) +e^x )/(e^(2x) +e^x +1)) dx Let u = e^x Ω = ∫_1 ^2 ((u^5 +2u^4 +u^2 +u)/(u^2 +u+1)). (du/u) Ω = ∫_1 ^2 ((u^4 +2u^3 +u+1)/(u^2 +u+1)) du Ω = ∫_1 ^2 (((u^2 +u−2)(u^2 +u+1)+(2u+1)+2)/(u^2 +u+1)) du Ω = ∫_1 ^2 (u^2 +u−2+((2u+1)/(u^2 +u+1))+(2/(u^2 +u+1))) du Ω_1 = ∫_1 ^2 (u^2 +u−2) du Ω_1 = [(u^3 /3)+(u^2 /2)−2u]_1 ^2 Ω_1 = ((8/3)+2−4)−((1/3)+(1/2)−2) Ω_1 = (4/6)−(−(7/6)) = ((11)/6) Ω_2 = ∫_1 ^2 ((2u+1)/(u^2 +u+1)) du Ω_2 = [ln∣u^2 +u+1∣]_1 ^2 Ω_2 = ln7−ln3 = ln(7/3) Ω_3 = ∫_1 ^2 (2/(u^2 +u+1)) du Ω_3 = ∫_1 ^2 (2/((u+(1/2))^2 +(3/4))) du Ω_3 = 2[(1/((√3)/2))arctan(((u+(1/2))/((√3)/2)))]_1 ^2 Ω_3 = (4/( (√3)))[arctan((2/( (√3)))(u+(1/2))]_1 ^2 Ω_3 = (4/( (√3)))(arctan((5/( (√3))))−arctan((3/( (√3))))) Ω_3 = (4/( (√3)))arctan((((5/( (√3)))−(3/( (√3))))/(1+(5/( (√3))).(3/( (√3)))))) Ω_3 = (4/( (√3)))arctan(((2/( (√3)))/6)) Ω_3 = (4/( (√3)))arctan((1/(3(√3)))) Ω =Ω_1 +Ω_2 +Ω_3 Ω = ((11)/6)+ln(7/3)+(4/( (√3)))arctan((1/(3(√3))))](Q144032.png)
Commented by BHOOPENDRA last updated on 20/Jun/21

| ||
Question and Answers Forum | ||
Question Number 144026 by mohammad17 last updated on 20/Jun/21 | ||
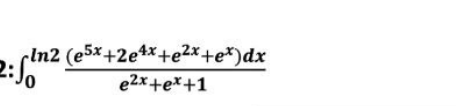 | ||
Commented by mohammad17 last updated on 20/Jun/21 | ||
 | ||
Answered by Olaf_Thorendsen last updated on 20/Jun/21 | ||
![Ω = ∫_0 ^(ln2) ((e^(5x) +2e^(4x) +e^(2x) +e^x )/(e^(2x) +e^x +1)) dx Let u = e^x Ω = ∫_1 ^2 ((u^5 +2u^4 +u^2 +u)/(u^2 +u+1)). (du/u) Ω = ∫_1 ^2 ((u^4 +2u^3 +u+1)/(u^2 +u+1)) du Ω = ∫_1 ^2 (((u^2 +u−2)(u^2 +u+1)+(2u+1)+2)/(u^2 +u+1)) du Ω = ∫_1 ^2 (u^2 +u−2+((2u+1)/(u^2 +u+1))+(2/(u^2 +u+1))) du Ω_1 = ∫_1 ^2 (u^2 +u−2) du Ω_1 = [(u^3 /3)+(u^2 /2)−2u]_1 ^2 Ω_1 = ((8/3)+2−4)−((1/3)+(1/2)−2) Ω_1 = (4/6)−(−(7/6)) = ((11)/6) Ω_2 = ∫_1 ^2 ((2u+1)/(u^2 +u+1)) du Ω_2 = [ln∣u^2 +u+1∣]_1 ^2 Ω_2 = ln7−ln3 = ln(7/3) Ω_3 = ∫_1 ^2 (2/(u^2 +u+1)) du Ω_3 = ∫_1 ^2 (2/((u+(1/2))^2 +(3/4))) du Ω_3 = 2[(1/((√3)/2))arctan(((u+(1/2))/((√3)/2)))]_1 ^2 Ω_3 = (4/( (√3)))[arctan((2/( (√3)))(u+(1/2))]_1 ^2 Ω_3 = (4/( (√3)))(arctan((5/( (√3))))−arctan((3/( (√3))))) Ω_3 = (4/( (√3)))arctan((((5/( (√3)))−(3/( (√3))))/(1+(5/( (√3))).(3/( (√3)))))) Ω_3 = (4/( (√3)))arctan(((2/( (√3)))/6)) Ω_3 = (4/( (√3)))arctan((1/(3(√3)))) Ω =Ω_1 +Ω_2 +Ω_3 Ω = ((11)/6)+ln(7/3)+(4/( (√3)))arctan((1/(3(√3))))](Q144032.png) | ||
| ||
Commented by BHOOPENDRA last updated on 20/Jun/21 | ||
 | ||