Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 144064 by 0731619 last updated on 21/Jun/21

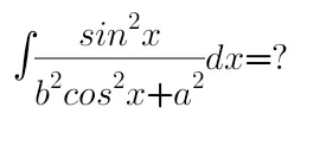
Answered by MJS_new last updated on 21/Jun/21

$$\mathrm{simply}\mathrm{let}t=\tan x$$$$\Rightarrow \mathrm{answer}\mathrm{is}$$$$-\frac{x}{b^2}+\frac{\sqrt{a^2+b^2}}{{ab}^2}\arctan \frac{a\tan x}{\sqrt{a^2+b^2}}+C$$

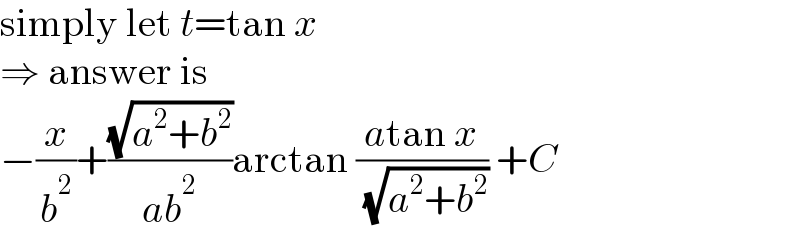
Commented by 0731619 last updated on 21/Jun/21

$$provethis$$

Commented by MJS_new last updated on 21/Jun/21

$$\mathrm{easy}\mathrm{to}\mathrm{prove}$$$$\frac{d}{dx}[-\frac{x}{b^2}]=-\frac{1}{b^2}$$$$\frac{d}{dx}\left[\frac{\sqrt{a^2+b^2}}{{ab}^2}\arctan \frac{a\tan x}{\sqrt{a^2+b^2}}\right]=$$$$=\frac{\sqrt{a^2+b^2}}{{ab}^2}\times \frac{a\sqrt{a^2+b^2}}{a^2+b^2+a^2{\tan }^{2}x}\times \frac{1}{{\cos }^{2}x}=$$$$=\frac{a^2+b^2}{b^2(a^2+b^2{\cos }^{2}x)}$$$$\frac{a^2+b^2}{b^2(a^2+b^2{\cos }^{2}x)}-\frac{1}{b^2}=\frac{{\sin }^{2}x}{a^2+b^2{\cos }^{2}x}q.e.d.$$

Commented by Dwaipayan Shikari last updated on 21/Jun/21

$$Q.E.D$$

Answered by mathmax by abdo last updated on 21/Jun/21

$$\mathrm{\Phi }=\int \frac{{\sin }^2\mathrm{x}}{{\mathrm{b}}^2{\cos }^2\mathrm{x}+{\mathrm{a}}^2}\mathrm{dx}=\int \frac{{\sin }^2\mathrm{xdx}}{{\mathrm{b}}^2({\cos }^2\mathrm{x}+\frac{{\mathrm{a}}^2}{{\mathrm{b}}^2})}=\frac{1}{{\mathrm{b}}^2}\int \frac{{\sin }^2\mathrm{x}}{\lambda +{\cos }^2\mathrm{x}}\mathrm{dx}$$$$\mathrm{with}\lambda =\frac{{\mathrm{a}}^2}{{\mathrm{b}}^2}>0$$$$\mathrm{f}\left(\lambda \right)=\int \frac{{\sin }^2\mathrm{x}}{\lambda +{\cos }^2\mathrm{x}}\mathrm{dx}=\int \frac{\frac{1-\cos \left(2\mathrm{x}\right)}{2}}{\lambda +\frac{1+\cos \left(2\mathrm{x}\right)}{2}}\mathrm{dx}$$$$=\int \frac{1-\cos \left(2\mathrm{x}\right)}{2\lambda +1+\cos \left(2\mathrm{x}\right)}\mathrm{dx}{=}_{2\mathrm{x}=\mathrm{t}}\frac{1}{2}\int \frac{1-\mathrm{cost}}{2\lambda +1+\mathrm{cost}}\mathrm{dt}$$$${=}_{\tan \left(\frac{\mathrm{t}}{2}\right)=\mathrm{y}}\frac{1}{2}\int \frac{1-\frac{1-{\mathrm{y}}^2}{1+{\mathrm{y}}^2}}{2\lambda +1+\frac{1-{\mathrm{y}}^2}{1+{\mathrm{y}}^2}}\times \frac{2\mathrm{dy}}{1+{\mathrm{y}}^2}$$$$=\int \frac{{2\mathrm{y}}^2}{(2\lambda +1)+(2\lambda +1){\mathrm{y}}^2+1-{\mathrm{y}}^2)}\frac{\mathrm{dy}}{(1+{\mathrm{y}}^2)}$$$$=2\int \frac{{\mathrm{y}}^2}{(1+{\mathrm{y}}^2)(2\lambda +2+2\lambda {\mathrm{y}}^2)}\mathrm{dy}=\int \frac{{\mathrm{y}}^2}{({\mathrm{y}}^2+1)(\lambda +1+{\mathrm{y}}^2)}\mathrm{dy}$$$$\mathrm{F}\left(\mathrm{y}\right)=\frac{{\mathrm{y}}^2}{({\mathrm{y}}^2+1)({\mathrm{y}}^2+\lambda +1)}=\frac{1}{\lambda }(\frac{{\mathrm{y}}^2}{{\mathrm{y}}^2+1}-\frac{{\mathrm{y}}^2}{{\mathrm{y}}^2+\lambda +1})$$$$=\frac{1}{\lambda }\{\frac{{\mathrm{y}}^2+1-1}{{\mathrm{y}}^2+1}-\frac{{\mathrm{y}}^2+\lambda +1-\lambda -1}{{\mathrm{y}}^2+\lambda +1}\}$$$$=\frac{1}{\lambda }\{-\frac{1}{{\mathrm{y}}^2+1}+\frac{\lambda +1}{{\mathrm{y}}^2+\lambda +1}\}$$

Commented by mathmax by abdo last updated on 21/Jun/21

$$\mathrm{f}\left(\lambda \right)=-\frac{1}{\lambda }\int \frac{\mathrm{dy}}{{\mathrm{y}}^2+1}+\frac{\lambda +1}{\lambda }\int \frac{\mathrm{dy}}{{\mathrm{y}}^2+\lambda +1}(\to \mathrm{y}=\sqrt{\lambda +1}\mathrm{z})$$$$=-\frac{1}{\lambda }\mathrm{arctany}+\frac{\lambda +1}{\lambda }\int \frac{\sqrt{\lambda +1}\mathrm{dz}}{(\lambda +1)(1+{\mathrm{z}}^2)}$$$$=-\frac{1}{\lambda }\mathrm{arctany}+\frac{\sqrt{\lambda +1}}{\lambda }\arctan \left(\frac{\mathrm{y}}{\sqrt{\lambda +1}}\right)+\mathrm{k}$$$$=-\frac{\mathrm{x}}{\lambda }+\frac{\sqrt{\lambda +1}}{\lambda }\arctan \left(\frac{1}{\sqrt{\lambda +1}}\mathrm{tanx}\right)+\mathrm{K}$$$$\mathrm{\Phi }=\frac{1}{{\mathrm{b}}^2}(-\frac{\mathrm{x}}{\frac{{\mathrm{a}}^2}{{\mathrm{b}}^2}}+\frac{{\mathrm{b}}^2}{{\mathrm{a}}^2}\sqrt{\frac{{\mathrm{a}}^2}{{\mathrm{b}}^2}+1}\arctan \left(\frac{1}{\sqrt{\frac{{\mathrm{a}}^2}{{\mathrm{b}}^2}+1}}\mathrm{tanx}\right)+\mathrm{K}$$$$=-\frac{\mathrm{x}}{{\mathrm{a}}^2}+\frac{1}{{\mathrm{a}}^2}\sqrt{\frac{{\mathrm{a}}^2+{\mathrm{b}}^2}{{\mathrm{b}}^2}}\arctan \left(\frac{\mid \mathrm{b}\mid }{\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}}\mathrm{tanx}\right)+\mathrm{K}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com