
Question and Answers Forum
Question Number 129710 by SOMEDAVONG last updated on 18/Jan/21
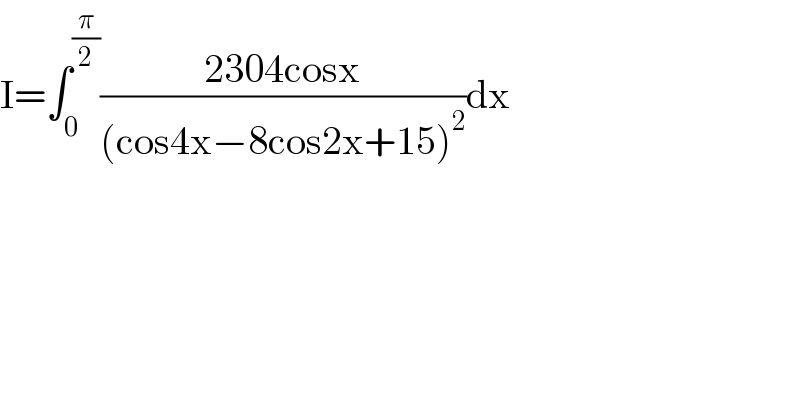
Answered by MJS_new last updated on 18/Jan/21
![2304∫((cos x)/((cos 4x −8cos 2x +15)^2 ))dx= [t=sin x → dx=(dt/(cos x))] =36∫(dt/((t^2 −t+1)^2 (t^2 +t+1)^2 ))= [Ostrogradski′s Method] =−((6t(t−1)(t+1))/((t^2 −t+1)(t^2 +t+1)))−6∫((t^2 −5)/((t^2 −t+1)(t^2 +t+1)))dt −6∫((t^2 −5)/((t^2 −t+1)(t^2 +t+1)))dt= =−3∫((6t−5)/(t^2 −t+1))dt+3∫((6t+5)/(t^2 +t+1))dt= =6∫(dt/(t^2 −t+1))−9∫((2t−1)/(t^2 −t+1))dt+6∫(dt/(t^2 +t+1))+9∫((2t+1)/(t^2 +t+1))dt= =4(√3)arctan (((√3)(2t−1))/3) −9ln (t^2 −t+1) +4(√3)arctan (((√3)(2t+1))/3) +9ln (t^2 +t+1) ⇒ we have 2304∫_0 ^(π/2) ((cos x)/((cos 4x −8cos 2x +15)^2 ))dx= [−((6t(t−1)(t+1))/((t^2 −t+1)(t^2 +t+1)))+4(√3)(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3))+9ln ((t^2 +t+1)/(t^2 −t+1))]_0 ^1 = =2π(√3)+9ln 3](Q129724.png)
| ||
Question and Answers Forum | ||
Question Number 129710 by SOMEDAVONG last updated on 18/Jan/21 | ||
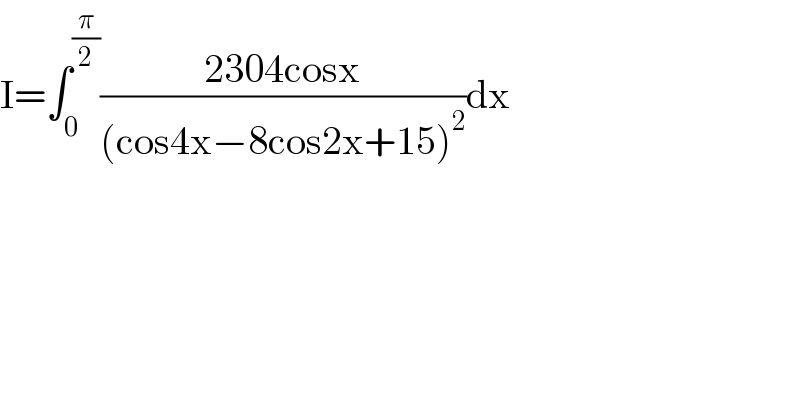 | ||
Answered by MJS_new last updated on 18/Jan/21 | ||
![2304∫((cos x)/((cos 4x −8cos 2x +15)^2 ))dx= [t=sin x → dx=(dt/(cos x))] =36∫(dt/((t^2 −t+1)^2 (t^2 +t+1)^2 ))= [Ostrogradski′s Method] =−((6t(t−1)(t+1))/((t^2 −t+1)(t^2 +t+1)))−6∫((t^2 −5)/((t^2 −t+1)(t^2 +t+1)))dt −6∫((t^2 −5)/((t^2 −t+1)(t^2 +t+1)))dt= =−3∫((6t−5)/(t^2 −t+1))dt+3∫((6t+5)/(t^2 +t+1))dt= =6∫(dt/(t^2 −t+1))−9∫((2t−1)/(t^2 −t+1))dt+6∫(dt/(t^2 +t+1))+9∫((2t+1)/(t^2 +t+1))dt= =4(√3)arctan (((√3)(2t−1))/3) −9ln (t^2 −t+1) +4(√3)arctan (((√3)(2t+1))/3) +9ln (t^2 +t+1) ⇒ we have 2304∫_0 ^(π/2) ((cos x)/((cos 4x −8cos 2x +15)^2 ))dx= [−((6t(t−1)(t+1))/((t^2 −t+1)(t^2 +t+1)))+4(√3)(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3))+9ln ((t^2 +t+1)/(t^2 −t+1))]_0 ^1 = =2π(√3)+9ln 3](Q129724.png) | ||
| ||