
Previous in Relation and Functions Next in Relation and Functions
Question Number 144220 by Mathspace last updated on 23/Jun/21
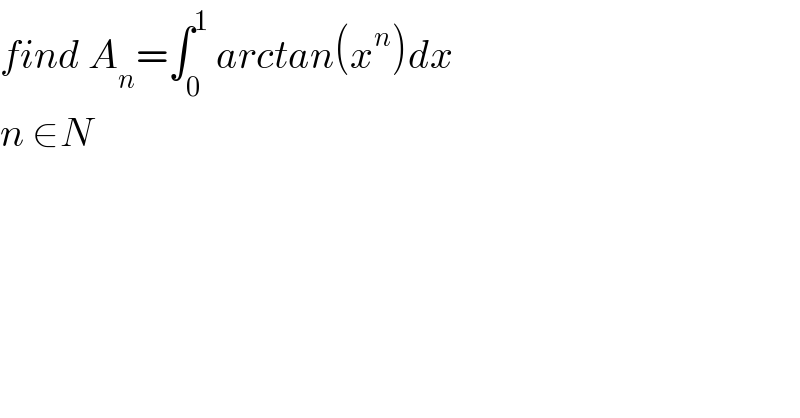
$${find}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({x}^{{n}} \right){dx} \\ $$$${n}\:\in{N} \\ $$
Answered by mathmax by abdo last updated on 26/Jun/21
![A_n =∫_0 ^1 arctan(x^n )dx ⇒A_n =[xarctan(x^n )]_0 ^1 −∫_0 ^1 x×((nx^(n−1) )/(1+x^(2n) ))dx =(π/4)−n∫_0 ^1 (x^n /(1+x^(2n) ))dx let decompose F(x)=(x^n /(1+x^(2n) )) x^(2n) =−1 ⇒x^(2n) =e^(i(2k+1)π) ⇒x_k =e^(i(((2k+1)π)/(2n))) and k∈[[0,2n−1]] F(x)=Σ_(k=0) ^(2n−1) (a_k /((x−x_k ))) a_k =(x_k ^n /(2nx_k ^(2n−1) )) =(x_k ^(n+1) /(2n x_k ^(2n) ))=−(1/(2n))x_k ^(n+1) ⇒F(x)=−(1/(2n))Σ_(=0) ^(2n−1) (x_k ^(n+1) /(x−x_k )) ⇒ ∫_0 ^1 (x^n /(1+x^(2n) ))dx=−(1/(2n))Σ_(k=0) ^(2n−1) x_k ^(n+1) ∫_0 ^1 (dx/(x−x_k )) =−(1/(2n))Σ_(k=0) ^(2n−1) x_k ^(n+1) [log(x−x_k )]_0 ^1 =−(1/(2n))Σ_(k=0) ^(2n−1) x_k ^(n+1) (log(1−x_k )−log(−x_k )) log here is compolex logarithm principal... ⇒ A_n =(π/4)−(1/2)Σ_(k=0) ^(2n−1) e^(i(((n+1)(2k+1)π)/(2n))) (log(1−x_k )−log(−x_k ))...](Q144507.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\mathrm{dx}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\left[\mathrm{xarctan}\left(\mathrm{x}^{\mathrm{n}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}×\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}−\mathrm{n}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\mathrm{dx}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} } \\ $$$$\mathrm{x}^{\mathrm{2n}} =−\mathrm{1}\:\Rightarrow\mathrm{x}^{\mathrm{2n}} \:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi} \:\Rightarrow\mathrm{x}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2n}}} \:\:\:\mathrm{and}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{2n}−\mathrm{1}\right]\right] \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)} \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}} }{\mathrm{2nx}_{\mathrm{k}} ^{\mathrm{2n}−\mathrm{1}} }\:=\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{1}} }{\mathrm{2n}\:\mathrm{x}_{\mathrm{k}} ^{\mathrm{2n}} }=−\frac{\mathrm{1}}{\mathrm{2n}}\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{1}} \:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{2n}}\sum_{=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{1}} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{2n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \mathrm{x}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}−\mathrm{x}_{\mathrm{k}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{1}} \left[\mathrm{log}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{1}} \left(\mathrm{log}\left(\mathrm{1}−\mathrm{x}_{\mathrm{k}} \right)−\mathrm{log}\left(−\mathrm{x}_{\mathrm{k}} \right)\right) \\ $$$$\mathrm{log}\:\mathrm{here}\:\mathrm{is}\:\mathrm{compolex}\:\mathrm{logarithm}\:\mathrm{principal}...\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2n}}} \:\left(\mathrm{log}\left(\mathrm{1}−\mathrm{x}_{\mathrm{k}} \right)−\mathrm{log}\left(−\mathrm{x}_{\mathrm{k}} \right)\right)... \\ $$
