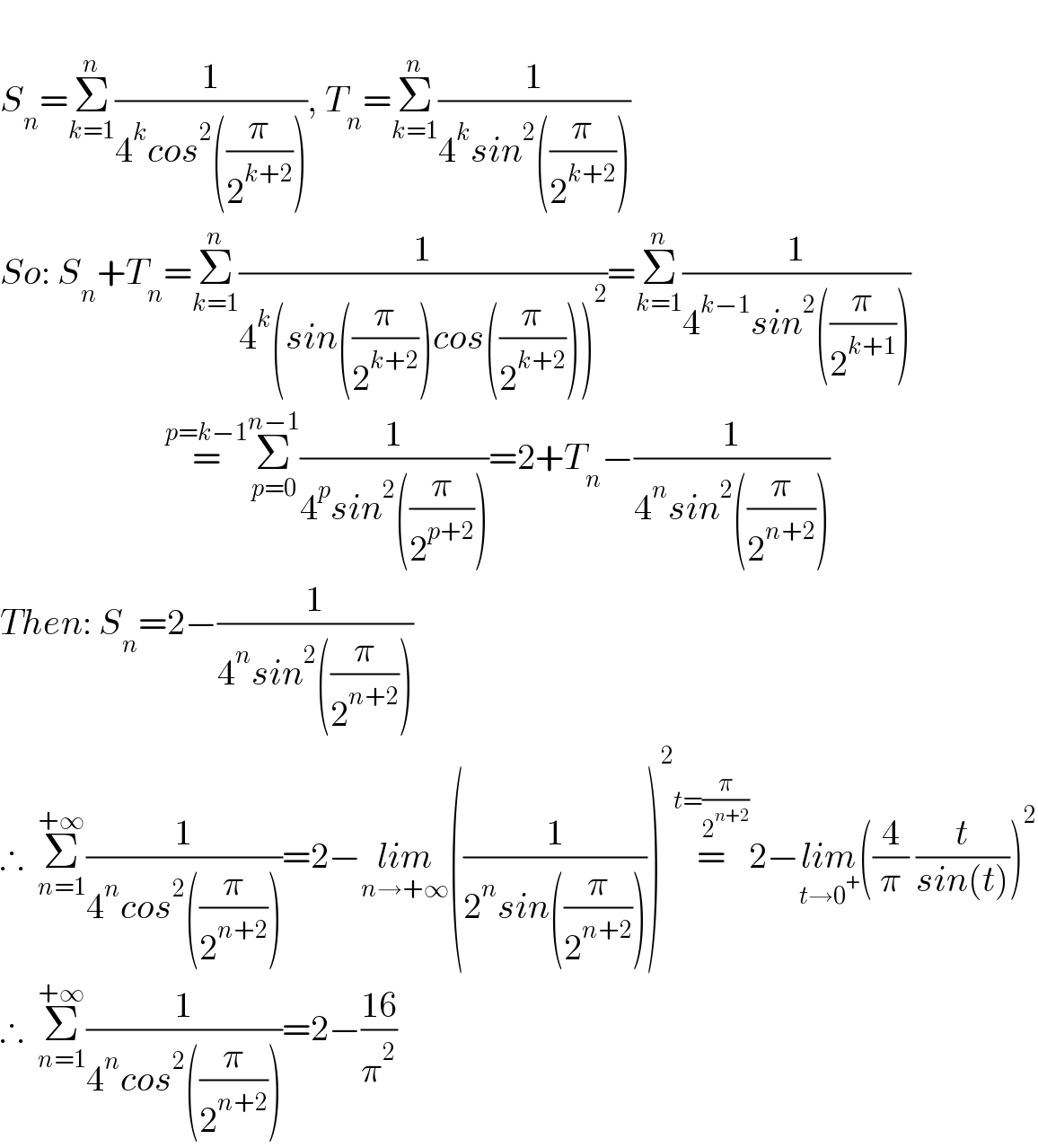
Question Number 144311 by mnjuly1970 last updated on 24/Jun/21
$$ \\ $$$$\:\:\:\:\:\:......\mathrm{Nice}\:\:\:\:....\:\:\:\:\mathrm{Calculus}...... \\ $$$$\:\:\:\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\::: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\Theta\::=\underset{{n}\:=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{\:{n}} \:{cos}^{\:\mathrm{2}} \:\left(\frac{\:\pi}{\:\mathrm{2}^{\:{n}\:+\:\mathrm{2}} }\:\right)\:\:}\:=? \\ $$$$\:\:\:\:.......... \\ $$
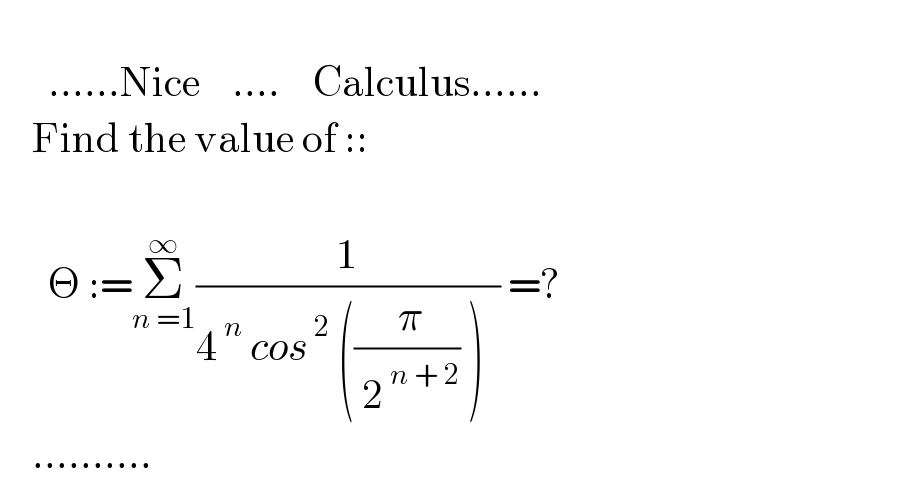
Commented by Kamel last updated on 24/Jun/21
$$ \\ $$$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{k}} {cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{k}+\mathrm{2}} }\right)},\:{T}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{k}} {sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{k}+\mathrm{2}} }\right)} \\ $$$${So}:\:{S}_{{n}} +{T}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{k}} \left({sin}\left(\frac{\pi}{\mathrm{2}^{{k}+\mathrm{2}} }\right){cos}\left(\frac{\pi}{\mathrm{2}^{{k}+\mathrm{2}} }\right)\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{k}−\mathrm{1}} {sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{k}+\mathrm{1}} }\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{{p}={k}−\mathrm{1}} {=}\underset{{p}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{p}} {sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{p}+\mathrm{2}} }\right)}=\mathrm{2}+{T}_{{n}} −\frac{\mathrm{1}}{\mathrm{4}^{{n}} {sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)} \\ $$$${Then}:\:{S}_{{n}} =\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4}^{{n}} {sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)} \\ $$$$\therefore\:\:\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{n}} {cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)}=\mathrm{2}−\underset{{n}\rightarrow+\infty} {{lim}}\left(\frac{\overset{} {\mathrm{1}}}{\mathrm{2}^{{n}} {sin}\left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)}\right)^{\mathrm{2}} \overset{{t}=\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }} {=}\mathrm{2}−\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\left(\frac{\mathrm{4}}{\pi}\:\frac{{t}}{{sin}\left({t}\right)}\right)^{\mathrm{2}} \\ $$$$\therefore\:\:\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{n}} {cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)}=\mathrm{2}−\frac{\mathrm{16}}{\pi^{\mathrm{2}} } \\ $$
Commented by mnjuly1970 last updated on 24/Jun/21
$${bravo}\:{mr}\:{kamel}\:{tashakor}.. \\ $$
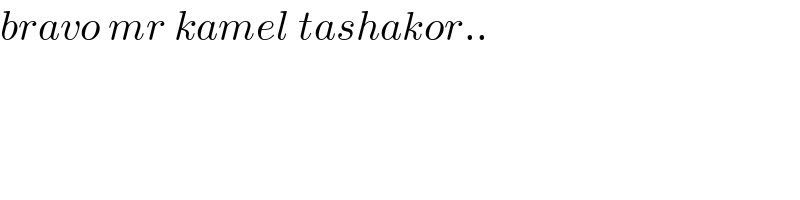
Answered by ArielVyny last updated on 24/Jun/21
![Θ=Σ_(n=1) ^∞ (1/4^n )[1+tg^2 ((π/2^(n+2) ))]=Σ_(n=1) ^∞ ((1/4))^n +Σ_(n=1) ^∞ ((tg^2 ((π/2^(n+2) )))/4^n ) Θ=(4/3)+Σ_(n=1) ^∞ ((1/4))^n tg^2 ((π/(4×2^n ))) posons ((1/2))^n =t Θ=(4/3)+Σ_(t=(1/2)) ^0 t^2 tg^2 ((π/4)t)=(4/3)−Σ_(t=0) ^(1/2) t^2 tg^2 ((π/4)t) Θ=(4/3)−(1/2)Σ_(t=0) ^1 t^2 tg^2 ((π/4)t) Θ=(4/3)−(1/2) Θ=(5/6)](Q144316.png)
$$\Theta=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{n}} }\left[\mathrm{1}+{tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)\right]=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} +\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{2}} }\right)}{\mathrm{4}^{{n}} } \\ $$$$\Theta=\frac{\mathrm{4}}{\mathrm{3}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} {tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}×\mathrm{2}^{{n}} }\right) \\ $$$${posons}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} ={t} \\ $$$$\Theta=\frac{\mathrm{4}}{\mathrm{3}}+\underset{{t}=\frac{\mathrm{1}}{\mathrm{2}}} {\overset{\mathrm{0}} {\sum}}{t}^{\mathrm{2}} {tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}{t}\right)=\frac{\mathrm{4}}{\mathrm{3}}−\underset{{t}=\mathrm{0}} {\overset{\frac{\mathrm{1}}{\mathrm{2}}} {\sum}}{t}^{\mathrm{2}} {tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}{t}\right) \\ $$$$\Theta=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{t}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}{t}^{\mathrm{2}} {tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}{t}\right) \\ $$$$\Theta=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Theta=\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Commented by mathmax by abdo last updated on 25/Jun/21
$$\mathrm{not}\:\mathrm{correct}! \\ $$
Answered by abdullahoudou last updated on 24/Jun/21
$$\mathrm{1}−\left(\mathrm{2}/\pi\right)^{\mathrm{2}} \\ $$
Commented by ArielVyny last updated on 24/Jun/21
$${you}\:{can}\:{show}\:{that}\:{please}? \\ $$