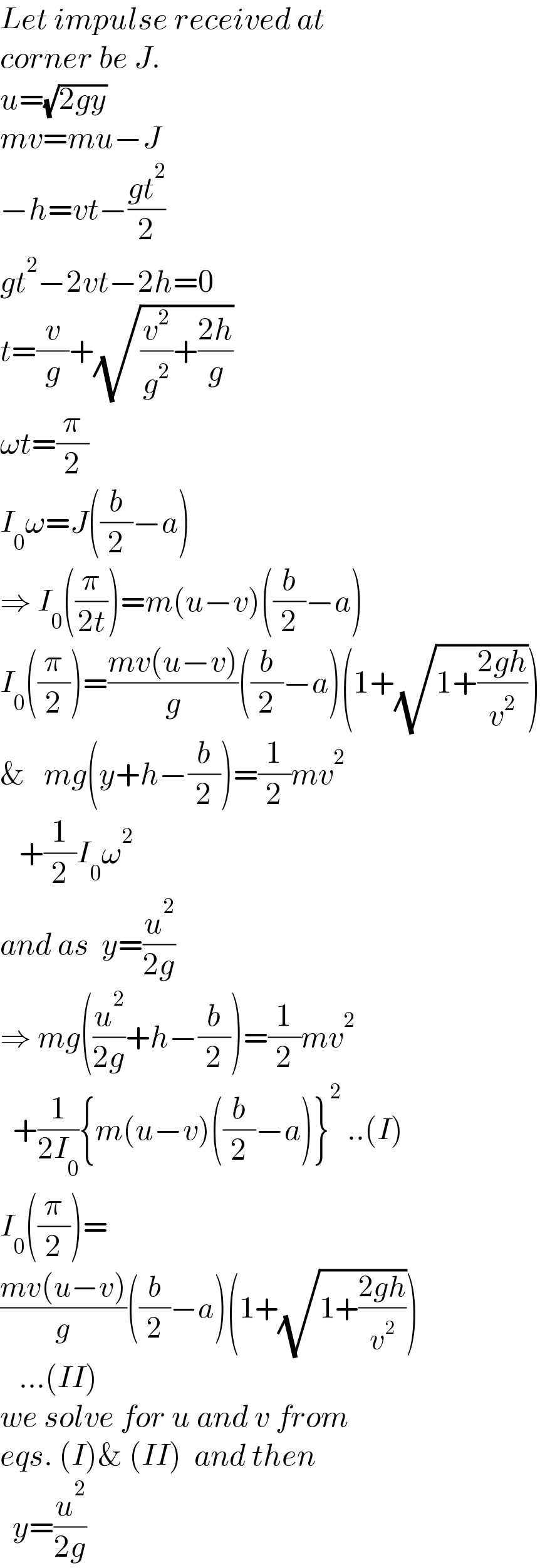Question Number 144496 by ajfour last updated on 25/Jun/21
Commented by ajfour last updated on 25/Jun/21
$${A}\:{rod}\:{is}\:{to}\:{be}\:{released}\: \\ $$$${horizontally}\:{at}\:{height}\:{y}\: \\ $$$${such}\:{that}\:{it}\:{hits}\:{ground} \\ $$$${in}\:{vertical}\:{orientation}. \\ $$$${Find}\:{y}\:{in}\:{terms}\:{of}\:{a},{b},{h}. \\ $$$${Rod}\:{suffers}\:{an}\:{elastic} \\ $$$${collision}\:{with}\:{the}\:{corner} \\ $$$${of}\:{table}. \\ $$
Answered by mr W last updated on 27/Jun/21
Commented by mr W last updated on 27/Jun/21
![u=(√(2gy)) (m/2)(u^2 −v^2 )=(1/2)×((mb^2 )/(12))×ω^2 ⇒12(u^2 −v^2 )=b^2 ω^2 ...(i) mu−P=mv P((b/2)−a)=((mb^2 )/(12))ω m(u−v)((b/2)−a)=((mb^2 )/(12))ω ⇒ 6(u−v)(b−2a)=b^2 ω ...(ii) (i)/(ii): ωb=((2(u+v))/(1−((2a)/b))) put into (ii): 6(u−v)(b−2a)=b((2(u+v))/(1−((2a)/b))) 3(1−((2a)/b))^2 (u−v)=u+v ⇒v=((3(1−((2a)/b))^2 −1)/(3(1−((2a)/b))^2 +1))u=βu v+u=((6(1−((2a)/b))^2 )/(3(1−((2a)/b))^2 +1))u ⇒bω=((12(1−((2a)/b)))/(3(1−((2a)/b))^2 +1))u=αu vt+(1/2)gt^2 =h−(b/2) 2vt+gt^2 =2h−b t=((−v+(√(v^2 +g(2h−b))))/g) ωt=(π/2) 2ω[(√(v^2 +g(2h−b)))−v]=πg ...(iii) 2α[u(√(β^2 u^2 +g(2h−b)))−βu^2 ]=πgb u(√(β^2 u^2 +g(2h−b)))=βu^2 +((πgb)/(2α)) (2h−b−((βπb)/α))u^2 =((π^2 gb^2 )/(4α^2 )) (2h−b−((βπb)/α))2gy=((π^2 gb^2 )/(4α^2 )) ⇒y=((π^2 b)/(8α^2 (((2h)/b)−1−((βπ)/α)))) with α=((12(1−((2a)/b)))/(3(1−((2a)/b))^2 +1)) β=((3(1−((2a)/b))^2 −1)/(3(1−((2a)/b))^2 +1))](Q144522.png)
$${u}=\sqrt{\mathrm{2}{gy}} \\ $$$$\frac{{m}}{\mathrm{2}}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mb}^{\mathrm{2}} }{\mathrm{12}}×\omega^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)={b}^{\mathrm{2}} \omega^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$${mu}−{P}={mv} \\ $$$${P}\left(\frac{{b}}{\mathrm{2}}−{a}\right)=\frac{{mb}^{\mathrm{2}} }{\mathrm{12}}\omega \\ $$$${m}\left({u}−{v}\right)\left(\frac{{b}}{\mathrm{2}}−{a}\right)=\frac{{mb}^{\mathrm{2}} }{\mathrm{12}}\omega \\ $$$$\Rightarrow\:\mathrm{6}\left({u}−{v}\right)\left({b}−\mathrm{2}{a}\right)={b}^{\mathrm{2}} \omega\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\omega{b}=\frac{\mathrm{2}\left({u}+{v}\right)}{\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}} \\ $$$${put}\:{into}\:\left({ii}\right): \\ $$$$\mathrm{6}\left({u}−{v}\right)\left({b}−\mathrm{2}{a}\right)={b}\frac{\mathrm{2}\left({u}+{v}\right)}{\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}} \\ $$$$\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} \left({u}−{v}\right)={u}+{v} \\ $$$$\Rightarrow{v}=\frac{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{1}}{u}=\beta{u} \\ $$$${v}+{u}=\frac{\mathrm{6}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{1}}{u} \\ $$$$\Rightarrow{b}\omega=\frac{\mathrm{12}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{1}}{u}=\alpha{u} \\ $$$${vt}+\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} ={h}−\frac{{b}}{\mathrm{2}} \\ $$$$\mathrm{2}{vt}+{gt}^{\mathrm{2}} =\mathrm{2}{h}−{b} \\ $$$${t}=\frac{−{v}+\sqrt{{v}^{\mathrm{2}} +{g}\left(\mathrm{2}{h}−{b}\right)}}{{g}} \\ $$$$\omega{t}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{2}\omega\left[\sqrt{{v}^{\mathrm{2}} +{g}\left(\mathrm{2}{h}−{b}\right)}−{v}\right]=\pi{g}\:\:\:...\left({iii}\right) \\ $$$$\mathrm{2}\alpha\left[{u}\sqrt{\beta^{\mathrm{2}} {u}^{\mathrm{2}} +{g}\left(\mathrm{2}{h}−{b}\right)}−\beta{u}^{\mathrm{2}} \right]=\pi{gb} \\ $$$${u}\sqrt{\beta^{\mathrm{2}} {u}^{\mathrm{2}} +{g}\left(\mathrm{2}{h}−{b}\right)}=\beta{u}^{\mathrm{2}} +\frac{\pi{gb}}{\mathrm{2}\alpha} \\ $$$$\left(\mathrm{2}{h}−{b}−\frac{\beta\pi{b}}{\alpha}\right){u}^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} {gb}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}{h}−{b}−\frac{\beta\pi{b}}{\alpha}\right)\mathrm{2}{gy}=\frac{\pi^{\mathrm{2}} {gb}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} } \\ $$$$\Rightarrow{y}=\frac{\pi^{\mathrm{2}} {b}}{\mathrm{8}\alpha^{\mathrm{2}} \left(\frac{\mathrm{2}{h}}{{b}}−\mathrm{1}−\frac{\beta\pi}{\alpha}\right)} \\ $$$${with}\: \\ $$$$\alpha=\frac{\mathrm{12}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\beta=\frac{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{b}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by ajfour last updated on 27/Jun/21
Thanks sir, our approach are the same, but you could bring it to completion; excellent soln.
Answered by ajfour last updated on 27/Jun/21
$${Let}\:{impulse}\:{received}\:{at}\: \\ $$$${corner}\:{be}\:{J}. \\ $$$${u}=\sqrt{\mathrm{2}{gy}} \\ $$$${mv}={mu}−{J} \\ $$$$−{h}={vt}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${gt}^{\mathrm{2}} −\mathrm{2}{vt}−\mathrm{2}{h}=\mathrm{0} \\ $$$${t}=\frac{{v}}{{g}}+\sqrt{\frac{{v}^{\mathrm{2}} }{{g}^{\mathrm{2}} }+\frac{\mathrm{2}{h}}{{g}}} \\ $$$$\omega{t}=\frac{\pi}{\mathrm{2}} \\ $$$${I}_{\mathrm{0}} \omega={J}\left(\frac{{b}}{\mathrm{2}}−{a}\right) \\ $$$$\Rightarrow\:{I}_{\mathrm{0}} \left(\frac{\pi}{\mathrm{2}{t}}\right)={m}\left({u}−{v}\right)\left(\frac{{b}}{\mathrm{2}}−{a}\right) \\ $$$${I}_{\mathrm{0}} \left(\frac{\pi}{\mathrm{2}}\right)=\frac{{mv}\left({u}−{v}\right)}{{g}}\left(\frac{{b}}{\mathrm{2}}−{a}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{2}{gh}}{{v}^{\mathrm{2}} }}\right) \\ $$$$\&\:\:\:{mg}\left({y}+{h}−\frac{{b}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{0}} \omega^{\mathrm{2}} \\ $$$${and}\:{as}\:\:{y}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}{g}} \\ $$$$\Rightarrow\:{mg}\left(\frac{{u}^{\mathrm{2}} }{\mathrm{2}{g}}+{h}−\frac{{b}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\:\:+\frac{\mathrm{1}}{\mathrm{2}{I}_{\mathrm{0}} }\left\{{m}\left({u}−{v}\right)\left(\frac{{b}}{\mathrm{2}}−{a}\right)\right\}^{\mathrm{2}} \:..\left({I}\right) \\ $$$${I}_{\mathrm{0}} \left(\frac{\pi}{\mathrm{2}}\right)= \\ $$$$\frac{{mv}\left({u}−{v}\right)}{{g}}\left(\frac{{b}}{\mathrm{2}}−{a}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{2}{gh}}{{v}^{\mathrm{2}} }}\right) \\ $$$$\:\:\:...\left({II}\right) \\ $$$${we}\:{solve}\:{for}\:{u}\:{and}\:{v}\:{from} \\ $$$${eqs}.\:\left({I}\right)\&\:\left({II}\right)\:\:{and}\:{then} \\ $$$$\:\:{y}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}{g}} \\ $$