Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 144500 by mathmax by abdo last updated on 25/Jun/21

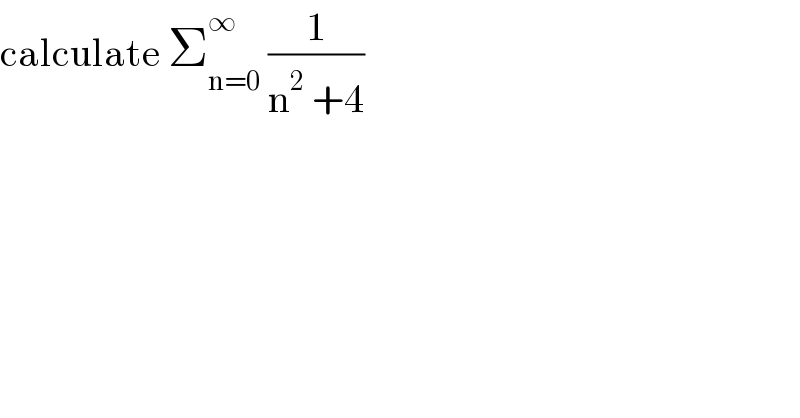
calculate Σ_(n=0) ^∞ (1/(n^2 +4))

$$\mathrm{calculate}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \:+\mathrm{4}} \\ $$

Answered by Dwaipayan Shikari last updated on 26/Jun/21

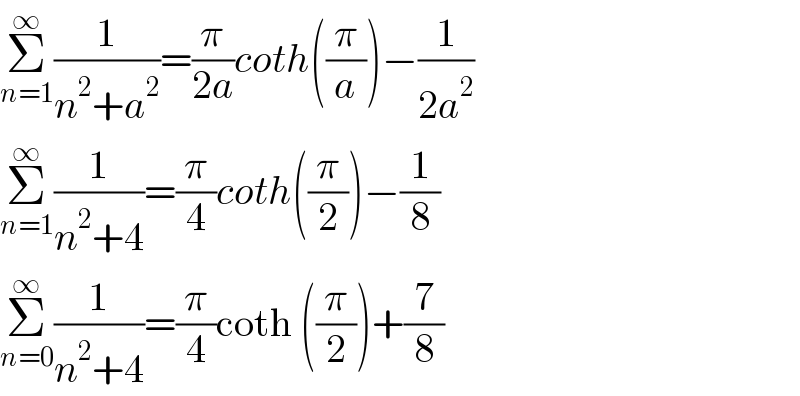
Σ_(n=1) ^∞ (1/(n^2 +a^2 ))=(π/(2a))coth((π/a))−(1/(2a^2 )) Σ_(n=1) ^∞ (1/(n^2 +4))=(π/4)coth((π/2))−(1/8) Σ_(n=0) ^∞ (1/(n^2 +4))=(π/4)coth ((π/2))+(7/8)

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{a}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{a}}{coth}\left(\frac{\pi}{{a}}\right)−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{4}}=\frac{\pi}{\mathrm{4}}{coth}\left(\frac{\pi}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{4}}=\frac{\pi}{\mathrm{4}}\mathrm{coth}\:\left(\frac{\pi}{\mathrm{2}}\right)+\frac{\mathrm{7}}{\mathrm{8}} \\ $$

Answered by ArielVyny last updated on 25/Jun/21

we have f(t)=(1/(t^2 +4)) positiv and decreasing in [0.∞] then ∫_0 ^∞ (1/(t^2 +4))dt=∫_0 ^∞ (1/(4(1+(t^2 /4))))dt=(1/4)∫_0 ^∞ (1/(1+(t^2 /4)))dt u=(t/4) du=(1/4)dt ∫_0 ^∞ (1/(1+u^2 ))du=[arctg]_0 ^∞ =(π/2)

$${we}\:{have}\:{f}\left({t}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{4}}\:{positiv}\:{and}\:{decreasing} \\ $$$${in}\:\left[\mathrm{0}.\infty\right]\:{then} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{4}}{dt}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\right)}{dt}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{4}}}{dt} \\ $$$${u}=\frac{{t}}{\mathrm{4}}\:{du}=\frac{\mathrm{1}}{\mathrm{4}}{dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}=\left[{arctg}\right]_{\mathrm{0}} ^{\infty} =\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 26/Jun/21

the Q is a sum not integral sir viny...

$$\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\mathrm{a}\:\mathrm{sum}\:\mathrm{not}\:\mathrm{integral}\:\mathrm{sir}\:\mathrm{viny}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com