let ϕ(x)=(1/(3+cosx)) developp f at fourier serie


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 144597 by mathmax by abdo last updated on 26/Jun/21

$let φ (x) = \frac{1}{3 + cosx}$ $developp f at fourier serie$
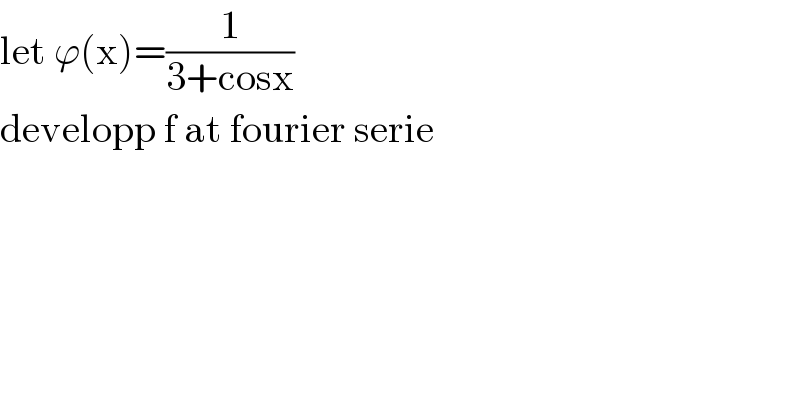
	Answered by Olaf_Thorendsen last updated on 26/Jun/21

	$a_{0} = \frac{1}{T} \int_{- \frac{T}{2}}^{+ \frac{T}{2}} f (x) d x$ $a_{0} = \frac{1}{2 π} \int_{- π}^{+ π} \frac{d x}{3 + \cos x}$ $a_{0} = \frac{1}{2 π} \int_{- π}^{+ π} \frac{d x}{3 + \cos x}$ $Let t = \tan \frac{x}{2}$ $a_{0} = \frac{1}{2 π} \int_{- \infty}^{+ \infty} \frac{1}{3 + \frac{1 - t^{2}}{1 + t^{2}}} . \frac{2 d t}{1 + t^{2}}$ $a_{0} = \frac{1}{π} \int_{- \infty}^{+ \infty} \frac{d t}{3 (1 + t^{2}) + (1 - t^{2})}$ $a_{0} = \frac{1}{π} \int_{- \infty}^{+ \infty} \frac{d t}{2 t^{2} + 4}$ $a_{0} = \frac{1}{2 π} \int_{- \infty}^{+ \infty} \frac{d t}{t^{2} + 2}$ $a_{0} = \frac{1}{2 π} {[\frac{1}{\sqrt{2}} \arctan \frac{t}{\sqrt{2}}]}_{- \infty}^{+ \infty}$ $a_{0} = \frac{1}{2 \sqrt{2} π} (\frac{π}{2}) = \frac{1}{4 \sqrt{2}}$ $a_{n} = \frac{2}{T} \int_{- \frac{T}{2}}^{+ \frac{T}{2}} f (x) \cos (\frac{2 π n x}{T}) d x$ $a_{n} = \frac{1}{π} \int_{- π}^{+ π} \frac{1}{3 + \cos x} \cos (n x) d x$ $a_{n + 2} + a_{n} = \frac{1}{π} \int_{- π}^{+ π} \frac{\cos ((n + 2) x) + \cos (n x)}{3 + \cos x} d x$ $a_{n + 2} + a_{n} = \frac{1}{π} \int_{- π}^{+ π} \frac{2 \cos ((n + 1) x) . \cos x}{3 + \cos x} d x$ $a_{n + 2} + a_{n} = \frac{2}{π} \int_{- π}^{+ π} \cos ((n + 1) x) d x$ $- \frac{2}{π} \int_{- π}^{+ π} \frac{3 \cos ((n + 1) x)}{3 + \cos x} d x$ $a_{n + 2} + a_{n} = \frac{2}{π} {[\frac{\sin ((n + 1) x)}{n + 1}]}_{- π}^{+ π} - 6 a_{n + 1}$ $a_{n + 2} + 6 a_{n + 1} + a_{n} = 0 (1)$ $a_{1} = \frac{1}{π} \int_{- π}^{+ π} \frac{\cos x}{3 + \cos x} d x$ $a_{1} = \frac{1}{π} \int_{- π}^{+ π} (1 - \frac{3}{3 + \cos x}) d x$ $a_{1} = \frac{1}{π} \int_{- π}^{+ π} d x - 6 a_{0}$ $a_{1} = 2 - \frac{6}{4 \sqrt{2}} = 2 - \frac{3}{2 \sqrt{2}}$ $(1) : r^{2} + 6 r + 1 = 0$ $r = \frac{- 6 \pm \sqrt{36 - 4}}{2} = - 3 \pm 2 \sqrt{2}$ $a_{n} = λ r_{1}^{n} + μ r_{2}^{n}$ $a_{0} = λ + μ = \frac{1}{4 \sqrt{2}}$ $a_{1} = λ r_{1} + μ r_{2} = 2 - \frac{3}{2 \sqrt{2}}$ $λ = \frac{\frac{r_{2}}{4 \sqrt{2}} - (2 - \frac{3}{2 \sqrt{2}})}{r_{2} - r_{1}}$ $λ = \frac{\frac{- 3 + 2 \sqrt{2}}{4 \sqrt{2}} - (2 - \frac{3}{2 \sqrt{2}})}{(- 3 + 2 \sqrt{2}) - (- 3 - 2 \sqrt{2)}}$ $λ = \frac{\frac{3}{4 \sqrt{2}} - \frac{3}{2}}{4 \sqrt{2}} = \frac{3}{32} (1 - 2 \sqrt{2})$ $μ = \frac{(2 - \frac{3}{2 \sqrt{2}}) - \frac{r_{1}}{4 \sqrt{2}}}{r_{2} - r_{1}}$ $μ = \frac{(2 - \frac{3}{2 \sqrt{2}}) - \frac{- 3 - 2 \sqrt{2}}{4 \sqrt{2}}}{(- 3 + 2 \sqrt{2}) - (- 3 - 2 \sqrt{2})}$ $μ = \frac{\frac{5}{2} - \frac{3}{4 \sqrt{2}}}{4 \sqrt{2}} = \frac{1}{32} (10 \sqrt{2} - 3)$ $a_{n} = λ r_{1}^{n} + μ r_{2}^{n}$ $a_{n} = \frac{3}{32} (1 - 2 \sqrt{2}) {(- 3 + 2 \sqrt{2})}^{n} + \frac{1}{32} (10 \sqrt{2} - 3) {(- 3 + 2 \sqrt{2})}^{n}$ $b_{n} = 0 \forall n (f is even)$ $f (x) = a_{0} + \underset{n = 1}{\sum^{\infty}} a_{n} \cos (\frac{2 π n x}{T})$ $f (x) = \frac{1}{4 \sqrt{2}} + \underset{n = 1}{\sum^{\infty}} a_{n} \cos (n x)$ $a_{n} = \frac{3}{32} (1 - 2 \sqrt{2}) {(- 3 + 2 \sqrt{2})}^{n} + \frac{1}{32} (10 \sqrt{2} - 3) {(- 3 + 2 \sqrt{2})}^{n}$
	Commented by mathmax by abdo last updated on 27/Jun/21

	$thank you sir$
	Answered by mathmax by abdo last updated on 27/Jun/21

	$φ (x) = \frac{1}{3 + cosx} = \frac{1}{3 + \frac{e^{ix} + e^{- ix}}{2}} = \frac{2}{6 + e^{ix} + e^{- ix}}$ $=_{e^{ix} = z} \frac{2}{6 + z + z^{- 1}} = \frac{2 z}{6 z + z^{2} + 1} = \frac{2 z}{z^{2} + 6 z + 1} = w (z)$ $Δ^{^{'}} = 3^{2} - 1 = 8 \Rightarrow z_{1} = - 3 + 2 \sqrt{2} and z_{2} = - 3 - 2 \sqrt{2}$ $\Rightarrow w (z) = \frac{2 z}{(z - z_{1}) (z - z_{2})} = 2 z (\frac{1}{z - z_{1}} - \frac{1}{z - z_{2}}) . \frac{1}{4 \sqrt{2}}$ $= \frac{1}{2 \sqrt{2}} (\frac{z}{z - z_{1}} - \frac{z}{z - z_{2}})$ $∣ \frac{z}{z_{1}} ∣ - 1 = \frac{1}{3 - 2 \sqrt{2}} - 1 = \frac{1 - 3 + 2 \sqrt{2}}{3 - 2 \sqrt{2}} = \frac{2 \sqrt{2} - 2}{3 - 2 \sqrt{2}} > 0 \Rightarrow∣ \frac{z}{z_{1}} ∣> 1$ $∣ \frac{z}{z_{2}} ∣ - 1 = \frac{1}{3 + 2 \sqrt{2}} - 1 = \frac{1 - 3 - 2 \sqrt{2}}{3 + 2 \sqrt{2}} < 0 \Rightarrow∣ \frac{z}{z_{2}} ∣< 1 \Rightarrow$ $w (z) = \frac{1}{2 \sqrt{2}} (\frac{1}{1 - \frac{z_{1}}{z}} - \frac{z}{z_{2}} \frac{1}{\frac{z}{z_{2}} - 1})$ $= \frac{1}{2 \sqrt{2}} (\sum_{n = 0}^{\infty} \frac{z_{1}^{n}}{z^{n}} + \frac{z}{z_{2}} \sum_{n = 0}^{\infty} \frac{z^{n}}{z_{2}^{n}})$ $= \frac{1}{2 \sqrt{2}} (\sum_{n = 0}^{\infty} {(- 3 + 2 \sqrt{2})}^{n} e^{- inx} + \frac{z}{z_{2}} \sum_{n = 0}^{\infty} \frac{1}{{(- 3 - 2 \sqrt{2})}^{n}} e^{inx})$ $= \frac{1}{2 \sqrt{2}} (\sum_{n = 0}^{\infty} {(- 1)}^{n} {(3 - 2 \sqrt{2})}^{n} e^{- inx} + \sum_{n = 0}^{\infty} {(- 1)}^{n + 1} {(3 - 2 \sqrt{2})}^{n + 1} e^{i (n + 1) x})$ $= \frac{1}{2 \sqrt{2}} (\sum_{n = 0}^{\infty} {(- 1)}^{n} {(3 - 2 \sqrt{2})}^{n} e^{- inx} + \sum_{n = 1}^{\infty} {(- 1)}^{n} {(3 - 2 \sqrt{2})}^{n} e^{inx})$ $= \frac{1}{2 \sqrt{2}} (1 + \sum_{n = 1}^{\infty} {(- 1)}^{n} {(3 - 2 \sqrt{2})}^{n} (2 \cos (nx)))$ $w (z) = \frac{1}{2 \sqrt{2}} + \frac{1}{\sqrt{2}} \sum_{n = 1}^{\infty} {(- 1)}^{n} {(3 - 2 \sqrt{2})}^{n} \cos (nx) = φ (x)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum