Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 144645 by mathdanisur last updated on 27/Jun/21

$$\underset{x\to 0}{lim}{\left(\frac{1+tanx}{1+sinx}\right)}^{\frac{1}{\mathit{s}\mathit{i}\mathit{n}\mathit{x}}}=?$$

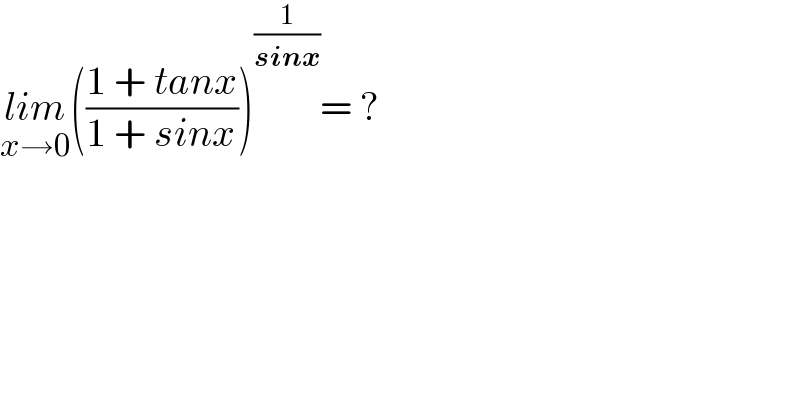
Answered by liberty last updated on 27/Jun/21

$$\underset{x\to 0}{\lim }{\left(\frac{1+\sin \mathrm{x}+\tan \mathrm{x}-\sin \mathrm{x}}{1+\sin \mathrm{x}}\right)}^{\frac{1}{\sin \mathrm{x}}}$$$$=\underset{x\to 0}{\lim }{(1+\frac{\tan \mathrm{x}-\sin \mathrm{x}}{1+\sin \mathrm{x}})}^{\frac{1}{\sin \mathrm{x}}}$$$$=\underset{x\to 0}{\lim }{\left[{(1+\frac{\tan \mathrm{x}-\sin \mathrm{x}}{1+\sin \mathrm{x}})}^{\frac{1+\sin \mathrm{x}}{\tan \mathrm{x}-\sin \mathrm{x}}}\right]}^{\frac{\tan \mathrm{x}-\sin \mathrm{x}}{\sin \mathrm{x}(1+\sin \mathrm{x})}}$$$$={\mathrm{e}}^{\underset{x\to 0}{\lim }\left(\frac{\tan \mathrm{x}-\sin \mathrm{x}}{\sin \mathrm{x}(1+\sin \mathrm{x})}\right)}$$$$={\mathrm{e}}^{\underset{x\to 0}{\lim }\left(\frac{\tan \mathrm{x}(1-\cos \mathrm{x})}{\sin \mathrm{x}(1+\sin \mathrm{x})}\right)}$$$$={\mathrm{e}}^{\frac{0}{1}}={\mathrm{e}}^0=1.$$

Commented by mathdanisur last updated on 27/Jun/21

$$alotcoolthankyouSir$$

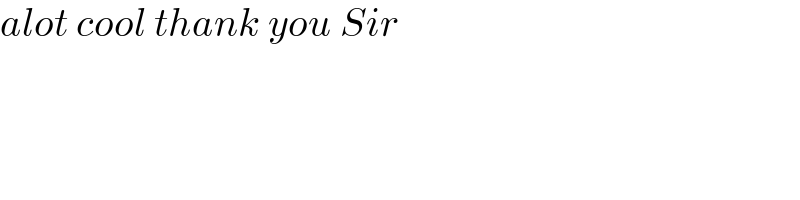
Answered by mathmax by abdo last updated on 27/Jun/21

$$\mathrm{f}\left(\mathrm{x}\right)={\left(\frac{1+\mathrm{tanx}}{1+\mathrm{sinx}}\right)}^{\frac{1}{\mathrm{sinx}}}\Rightarrow \mathrm{f}\left(\mathrm{x}\right)={\left(\frac{1+\mathrm{sinx}+\mathrm{tanx}-\mathrm{sinx}}{1+\mathrm{sinx}}\right)}^{\frac{1}{\mathrm{sinx}}}$$$$={(1+\frac{\mathrm{tanx}-\mathrm{sinx}}{1+\mathrm{sinx}})}^{\frac{1}{\mathrm{sinx}}}={\mathrm{e}}^{\frac{1}{\mathrm{sinx}}\log (1+\frac{\mathrm{tanx}-\mathrm{sinx}}{1+\mathrm{sinx}})}\mathrm{we}\mathrm{have}$$$$\log (1+\frac{\mathrm{tanx}-\mathrm{sinx}}{1+\mathrm{sinx}})\sim \frac{\mathrm{tanx}-\mathrm{sinx}}{1+\mathrm{sinx}}\Rightarrow \frac{1}{\mathrm{sinx}}\log (...)\sim \frac{\mathrm{tanx}-\mathrm{sinx}}{\mathrm{sinx}(1+\mathrm{sinx})}$$$$\sim \frac{\mathrm{x}+\frac{{\mathrm{x}}^3}{3}-(\mathrm{x}-\frac{{\mathrm{x}}^3}{6})}{\mathrm{x}(1+\mathrm{x})}=\frac{{\mathrm{x}}^3}{6\mathrm{x}(1+\mathrm{x})}\sim \frac{{\mathrm{x}}^2}{6(1+\mathrm{x})}\to 0(\mathrm{x}\to 0)\Rightarrow$$$${\lim }_{\mathrm{x}\to 0}\mathrm{f}\left(\mathrm{x}\right)={\mathrm{e}}^0=1$$

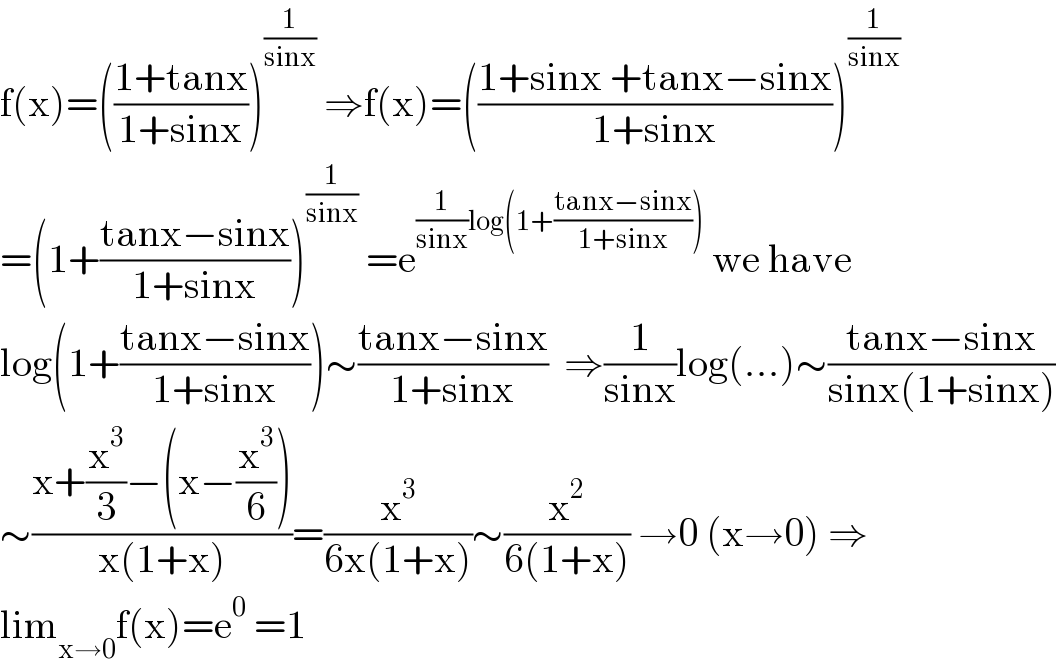
Commented by mathdanisur last updated on 27/Jun/21

$$ThanksSiralotcool$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com