
Question and Answers Forum
Question Number 144829 by mathlove last updated on 29/Jun/21
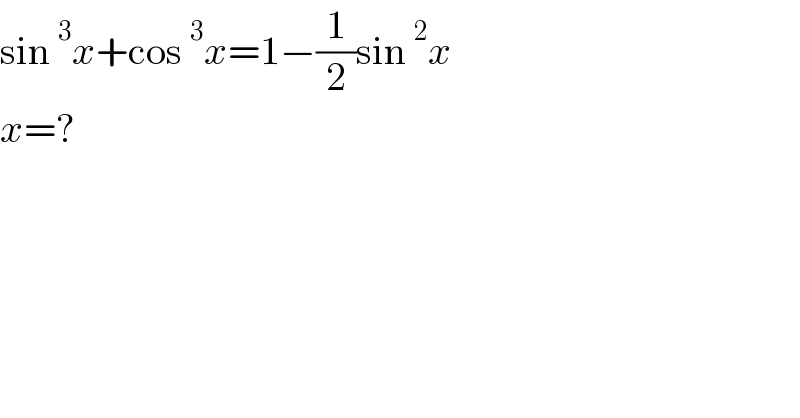
Answered by ajfour last updated on 29/Jun/21
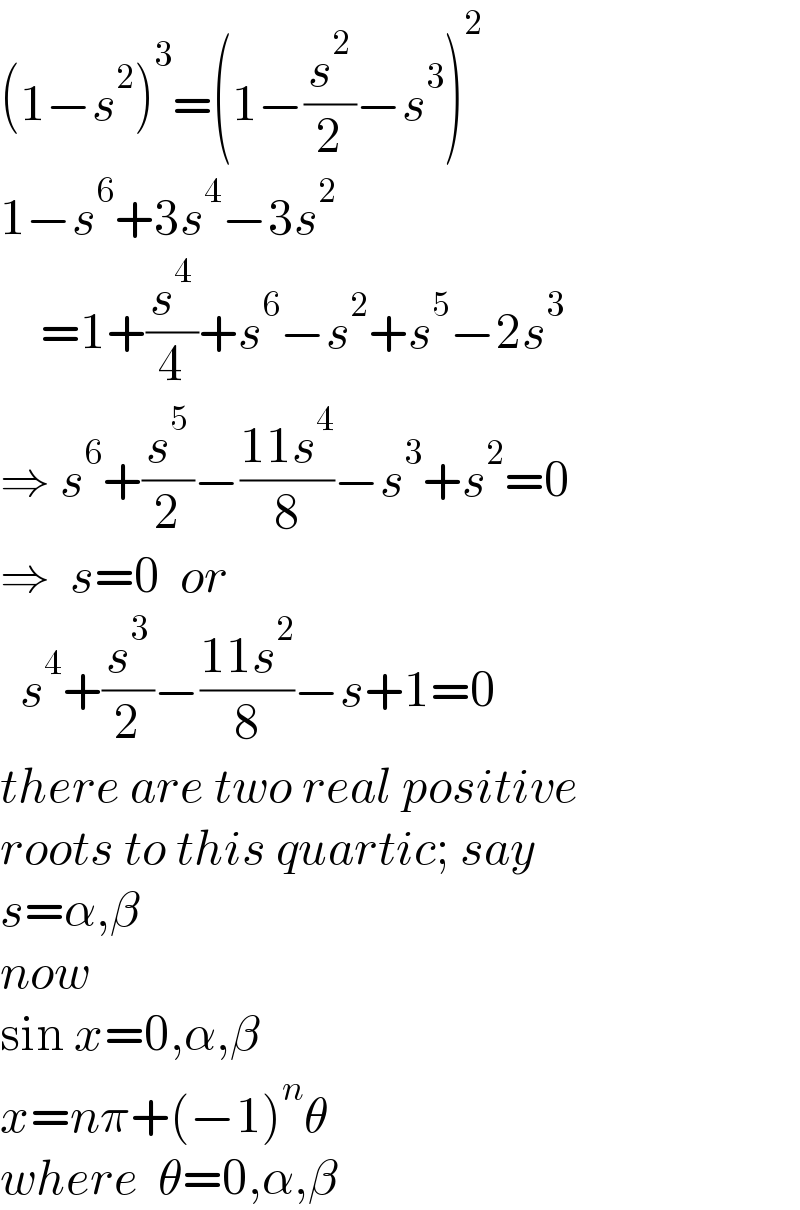
Answered by liberty last updated on 29/Jun/21
![sin^3 x+cos^3 x=sin^2 x+cos^2 x−(1/2)sin^2 x sin^3 x+cos^3 x=(1/2)sin^2 x+cos^2 x cos^3 x−cos^2 x=(1/2)sin^2 x−sin^3 x cos^2 x(cos x−1)=sin^2 x((1/2)−sin x) cos^2 x(−2sin^2 (1/2)x)=sin^2 x((1/2)−2sin (1/2)xcos (1/2)x) let tan (x/2)=t⇒tan x=((2t)/(1−t^2 )) ⇒−2((t^2 /(1+t^2 )))=(((2t)/(1−t^2 )))((1/2)−((2t)/(1+t^2 ))) ⇒((−2t^2 )/(1+t^2 ))= (((2t)/(1−t^2 )))(((1+t^2 −4t)/(2(1+t^2 )))) ⇒(((2t)/(1+t^2 )))[((t^2 −4t+1)/(2−2t^2 )) +t ]=0 ⇒(((2t)/(1+t^2 )))[((t^2 −4t+1+2t−2t^3 )/(2−2t^2 ))]=0 ⇒(((2t)/(1+t^2 )))(((2t^3 −t^2 +2t−1)/(2−2t^2 )))=0 we get t=0 ⇒tan (x/2) = 0 →(x/2) = 0+kπ ⇒x= 2kπ ; k∈Z for 2t^3 −t^2 +2t−1=0 test t=(1/2)→(1/4)−(1/4)+1−1=0 (valid) ⇒factorise (2t−1)(t^2 +1)=0 ⇒tan (x/2)=(1/2) ; (x/2)= arctan ((1/2))+kπ ⇒x=2arctan ((1/2))+2kπ](Q144834.png)
| ||
Question and Answers Forum | ||
Question Number 144829 by mathlove last updated on 29/Jun/21 | ||
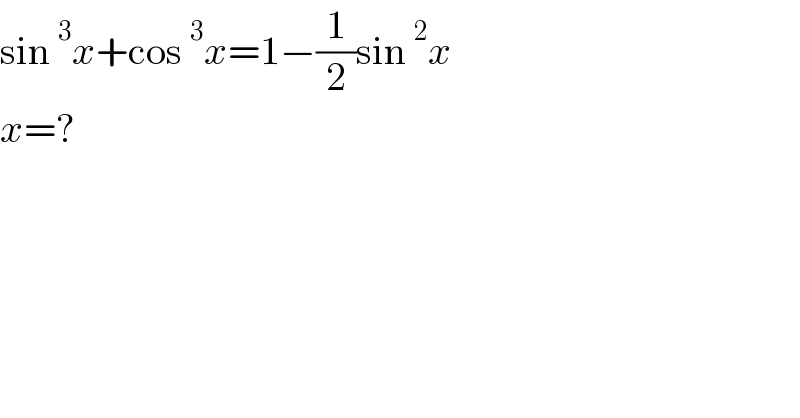 | ||
Answered by ajfour last updated on 29/Jun/21 | ||
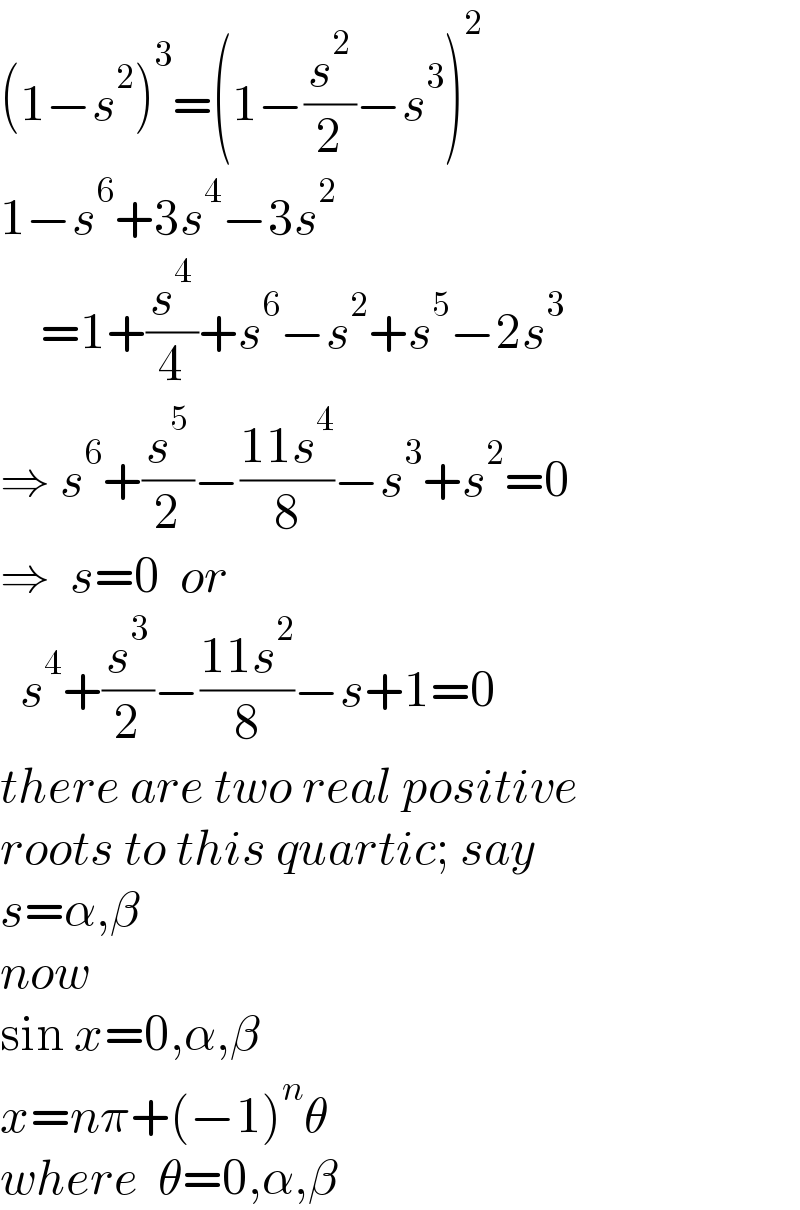 | ||
| ||
Answered by liberty last updated on 29/Jun/21 | ||
![sin^3 x+cos^3 x=sin^2 x+cos^2 x−(1/2)sin^2 x sin^3 x+cos^3 x=(1/2)sin^2 x+cos^2 x cos^3 x−cos^2 x=(1/2)sin^2 x−sin^3 x cos^2 x(cos x−1)=sin^2 x((1/2)−sin x) cos^2 x(−2sin^2 (1/2)x)=sin^2 x((1/2)−2sin (1/2)xcos (1/2)x) let tan (x/2)=t⇒tan x=((2t)/(1−t^2 )) ⇒−2((t^2 /(1+t^2 )))=(((2t)/(1−t^2 )))((1/2)−((2t)/(1+t^2 ))) ⇒((−2t^2 )/(1+t^2 ))= (((2t)/(1−t^2 )))(((1+t^2 −4t)/(2(1+t^2 )))) ⇒(((2t)/(1+t^2 )))[((t^2 −4t+1)/(2−2t^2 )) +t ]=0 ⇒(((2t)/(1+t^2 )))[((t^2 −4t+1+2t−2t^3 )/(2−2t^2 ))]=0 ⇒(((2t)/(1+t^2 )))(((2t^3 −t^2 +2t−1)/(2−2t^2 )))=0 we get t=0 ⇒tan (x/2) = 0 →(x/2) = 0+kπ ⇒x= 2kπ ; k∈Z for 2t^3 −t^2 +2t−1=0 test t=(1/2)→(1/4)−(1/4)+1−1=0 (valid) ⇒factorise (2t−1)(t^2 +1)=0 ⇒tan (x/2)=(1/2) ; (x/2)= arctan ((1/2))+kπ ⇒x=2arctan ((1/2))+2kπ](Q144834.png) | ||
| ||