Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 144839 by mathdanisur last updated on 29/Jun/21

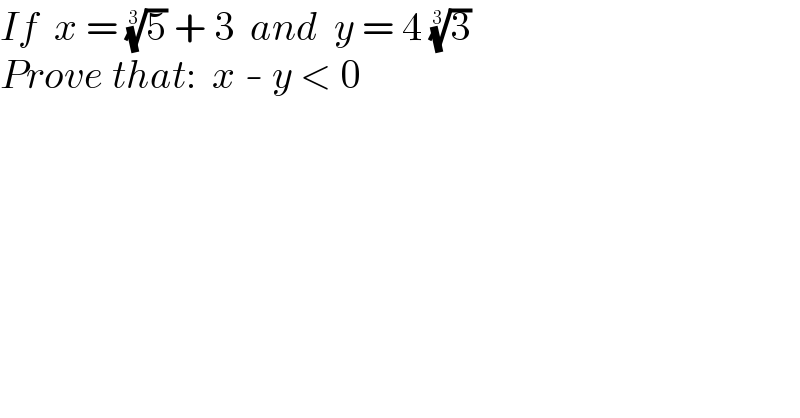
If x = (5)^(1/3) + 3 and y = 4 (3)^(1/3) Prove that: x - y < 0

$${If}\:\:{x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{5}}\:+\:\mathrm{3}\:\:{and}\:\:{y}\:=\:\mathrm{4}\:\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$ $${Prove}\:{that}:\:\:{x}\:-\:{y}\:<\:\mathrm{0} \\ $$

Answered by ajfour last updated on 29/Jun/21

(x−3)^3 =5 y^3 =192 ...(i) x^3 −9x^2 +27x−27=5 ...(ii) subtracting ..(i) from (ii) (x−y){[(x−y)+((3y)/2)]^2 +((3y^2 )/4)} +9x^2 +27x+160=0 for x>0, above eq. is true only if x−y<0 ; (and above eq. is of course true).

$$\left({x}−\mathrm{3}\right)^{\mathrm{3}} =\mathrm{5} \\ $$ $${y}^{\mathrm{3}} =\mathrm{192}\:\:\:...\left({i}\right) \\ $$ $${x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{27}=\mathrm{5}\:\:\:...\left({ii}\right) \\ $$ $${subtracting}\:\:..\left({i}\right)\:\:{from}\:\left({ii}\right) \\ $$ $$\left({x}−{y}\right)\left\{\left[\left({x}−{y}\right)+\frac{\mathrm{3}{y}}{\mathrm{2}}\right]^{\mathrm{2}} +\frac{\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{4}}\right\} \\ $$ $$+\mathrm{9}{x}^{\mathrm{2}} +\mathrm{27}{x}+\mathrm{160}=\mathrm{0} \\ $$ $${for}\:{x}>\mathrm{0},\:\:\:{above}\:{eq}.\:{is}\:{true} \\ $$ $${only}\:{if}\:\:{x}−{y}<\mathrm{0}\:;\:\left({and}\:{above}\right. \\ $$ $$\left.{eq}.\:{is}\:{of}\:{course}\:{true}\right). \\ $$

Commented bymathdanisur last updated on 29/Jun/21

thankyou Sir cool

$${thankyou}\:{Sir}\:{cool} \\ $$

Answered by Rakshay last updated on 29/Jun/21

suppose x−y≥0 i.e ^3 (√5)+3−4^3 (√3)≥0 ⇒4^3 (√3)−^3 (√5)≤3.....(1) ⇒ (4^3 (√3)−^3 (√5))^3 ≤27 (64)(3)−(5)−3(4 )(^3 (√(15)))(4^3 (√3)−^3 (√5))≤27 204−5−12(^3 (√(15)))(4^3 (√3) −^3 (√5))≤27 ⇒172−12(^3 (√(15)))(4^3 (√3)−^3 (√5))≤0 ⇒((172)/(12))≤(^3 (√(15)))(4^3 (√3)−^3 (√5))≤(3)(^3 (√(15))) ⇒((172)/(36))≤^3 (√(15))( which isn′t true) so our supposition is wrong, thus, x−y<0

$${suppose}\:{x}−{y}\geqslant\mathrm{0} \\ $$ $${i}.{e}\:\:\:\:\:\:\:^{\mathrm{3}} \sqrt{\mathrm{5}}+\mathrm{3}−\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}\geqslant\mathrm{0} \\ $$ $$\:\:\:\:\:\:\:\Rightarrow\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\leqslant\mathrm{3}.....\left(\mathrm{1}\right) \\ $$ $$\Rightarrow\:\:\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)^{\mathrm{3}} \leqslant\mathrm{27} \\ $$ $$\:\:\:\left(\mathrm{64}\right)\left(\mathrm{3}\right)−\left(\mathrm{5}\right)−\mathrm{3}\left(\mathrm{4}\:\right)\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\mathrm{27} \\ $$ $$\mathrm{204}−\mathrm{5}−\mathrm{12}\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}\:−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\mathrm{27} \\ $$ $$\Rightarrow\mathrm{172}−\mathrm{12}\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\mathrm{0} \\ $$ $$\Rightarrow\frac{\mathrm{172}}{\mathrm{12}}\leqslant\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\left(\mathrm{3}\right)\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right) \\ $$ $$\Rightarrow\frac{\mathrm{172}}{\mathrm{36}}\leqslant^{\mathrm{3}} \sqrt{\mathrm{15}}\left(\:{which}\:{isn}'{t}\:{true}\right)\: \\ $$ $${so}\:{our}\:{supposition}\:{is}\:{wrong},\:{thus}, \\ $$ $${x}−{y}<\mathrm{0} \\ $$

Commented bymathdanisur last updated on 29/Jun/21

thanks Sir cool

$${thanks}\:{Sir}\:{cool} \\ $$

Answered by mr W last updated on 29/Jun/21

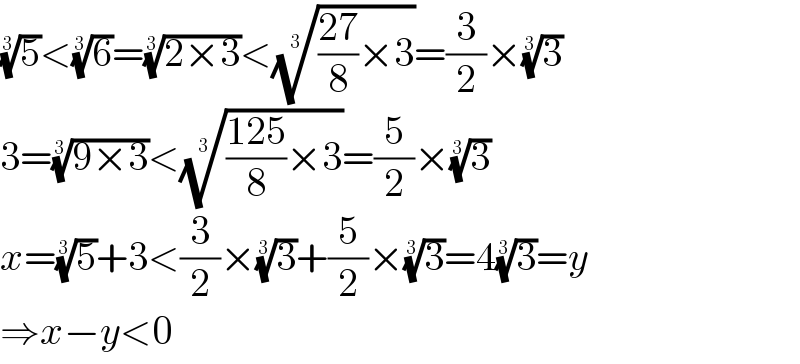
(5)^(1/3) <(6)^(1/3) =((2×3))^(1/3) <((((27)/8)×3))^(1/3) =(3/2)×(3)^(1/3) 3=((9×3))^(1/3) <((((125)/8)×3))^(1/3) =(5/2)×(3)^(1/3) x=(5)^(1/3) +3<(3/2)×(3)^(1/3) +(5/2)×(3)^(1/3) =4(3)^(1/3) =y ⇒x−y<0

$$\sqrt[{\mathrm{3}}]{\mathrm{5}}<\sqrt[{\mathrm{3}}]{\mathrm{6}}=\sqrt[{\mathrm{3}}]{\mathrm{2}×\mathrm{3}}<\sqrt[{\mathrm{3}}]{\frac{\mathrm{27}}{\mathrm{8}}×\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$ $$\mathrm{3}=\sqrt[{\mathrm{3}}]{\mathrm{9}×\mathrm{3}}<\sqrt[{\mathrm{3}}]{\frac{\mathrm{125}}{\mathrm{8}}×\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$ $${x}=\sqrt[{\mathrm{3}}]{\mathrm{5}}+\mathrm{3}<\frac{\mathrm{3}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}}=\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{3}}={y} \\ $$ $$\Rightarrow{x}−{y}<\mathrm{0} \\ $$

Commented bymathdanisur last updated on 29/Jun/21

cool Sir thanks

$${cool}\:{Sir}\:{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com