
Question and Answers Forum
Question Number 144924 by qaz last updated on 30/Jun/21
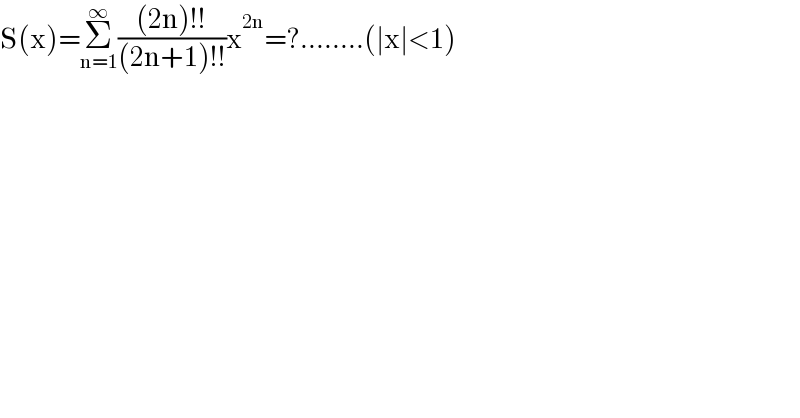
Answered by Ar Brandon last updated on 30/Jun/21
![(2n+1)!!=(((2n+1)!)/((2n)!!)) S(x)=Σ_(n=1) ^∞ ((((2n)!!)^2 )/((2n+1)!))x^(2n) =Σ_(n=1) ^∞ ((2^(2n) (n!)^2 )/((2n+1)!))x^(2n) =Σ_(n=1) ^∞ (2x)^(2n) β(n+1,n+1)=∫_0 ^1 Σ_(n=1) ^∞ (2x)^(2n) t^n (1−t)^n dt =∫_0 ^1 Σ_(n=1) ^∞ (4x^2 t−4x^2 t^2 )^n dt=∫_0 ^1 (dt/(4x^2 t^2 −4x^2 t+1))−1 =(1/(4x^2 ))∫_0 ^1 (dt/((t−(1/2))^2 +((1−x^2 )/(4x^2 ))))−1=(1/(4x^2 ))∙((2∣x∣)/( (√(1−x^2 ))))[tan^(−1) (((2∣x∣t−∣x∣)/( (√(1−x^2 )))))]_0 ^1 −1 =((∣x∣)/(x^2 (√(1−x^2 ))))tan^(−1) (((∣x∣)/( (√(1−x^2 )))))−1](Q144938.png)
Commented byqaz last updated on 30/Jun/21

Commented byAr Brandon last updated on 30/Jun/21
Je vous en prie !
| ||
Question and Answers Forum | ||
Question Number 144924 by qaz last updated on 30/Jun/21 | ||
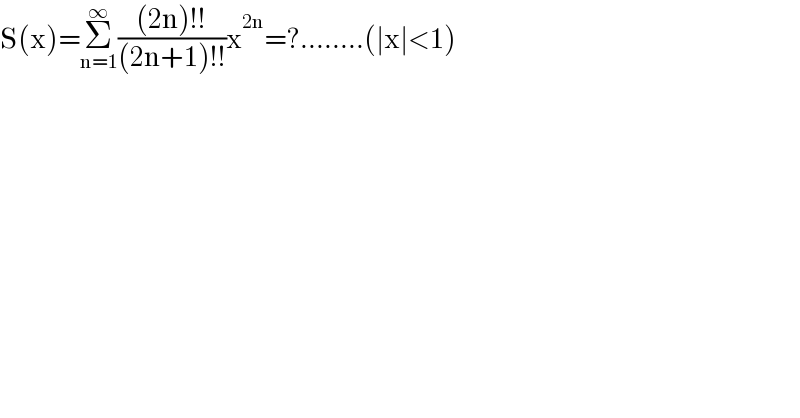 | ||
Answered by Ar Brandon last updated on 30/Jun/21 | ||
![(2n+1)!!=(((2n+1)!)/((2n)!!)) S(x)=Σ_(n=1) ^∞ ((((2n)!!)^2 )/((2n+1)!))x^(2n) =Σ_(n=1) ^∞ ((2^(2n) (n!)^2 )/((2n+1)!))x^(2n) =Σ_(n=1) ^∞ (2x)^(2n) β(n+1,n+1)=∫_0 ^1 Σ_(n=1) ^∞ (2x)^(2n) t^n (1−t)^n dt =∫_0 ^1 Σ_(n=1) ^∞ (4x^2 t−4x^2 t^2 )^n dt=∫_0 ^1 (dt/(4x^2 t^2 −4x^2 t+1))−1 =(1/(4x^2 ))∫_0 ^1 (dt/((t−(1/2))^2 +((1−x^2 )/(4x^2 ))))−1=(1/(4x^2 ))∙((2∣x∣)/( (√(1−x^2 ))))[tan^(−1) (((2∣x∣t−∣x∣)/( (√(1−x^2 )))))]_0 ^1 −1 =((∣x∣)/(x^2 (√(1−x^2 ))))tan^(−1) (((∣x∣)/( (√(1−x^2 )))))−1](Q144938.png) | ||
| ||
Commented byqaz last updated on 30/Jun/21 | ||
 | ||
Commented byAr Brandon last updated on 30/Jun/21 | ||
Je vous en prie ! | ||