
Question and Answers Forum
Question Number 14535 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 02/Jun/17

Commented by ajfour last updated on 03/Jun/17

Commented by mrW1 last updated on 02/Jun/17
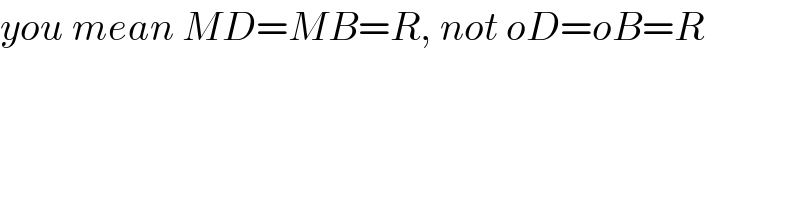
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17

Answered by ajfour last updated on 03/Jun/17
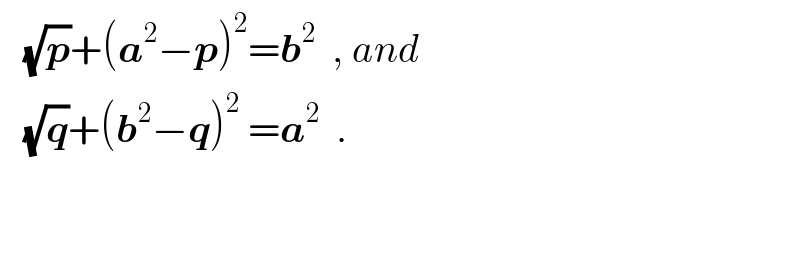
Commented by ajfour last updated on 03/Jun/17

Commented by ajfour last updated on 03/Jun/17
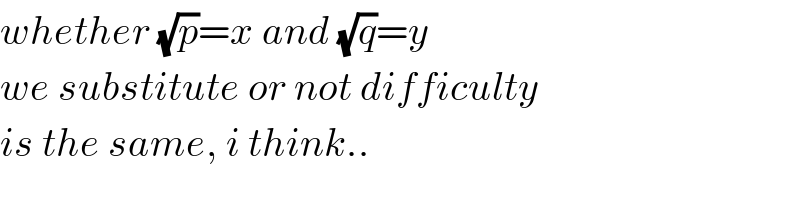
Commented by ajfour last updated on 03/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
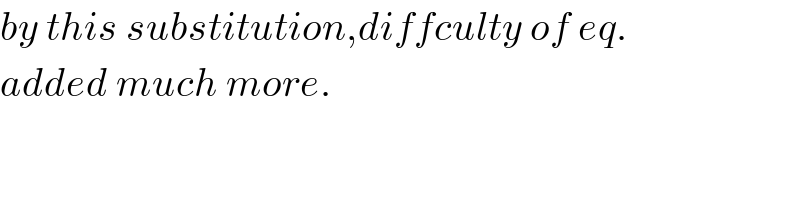
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17

Commented by ajfour last updated on 03/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17

Answered by mr W last updated on 05/Aug/19
![let x=(√p), y=(√q) let u=a^2 , v=b^2 x^2 +y=u x+y^2 =v x+(u−x^2 )^2 =v ⇒x^4 −2ux^2 +x+u^2 −v=0 trying to use method from ajfour sir: a=−2u b=1 c=u^2 −v ⇒x^2 −px+(1/2)(−2u+p^2 +(1/p))=0 ⇒x=(1/2)(p±(√(4u−p^2 −(2/p)))) where p^2 =P with P^3 −4uP^2 +4vP−1=0 let P=Q+((4u)/3) Q^3 +3(((4u)/3))Q^2 +3(((4u)/3))^2 Q+(((4u)/3))^3 −4u[Q^2 +2(((4u)/3))Q+(((4u)/3))^2 ]+4v(Q+((4u)/3))−1=0 Q^3 +4(v−((4u^2 )/3))Q+((16uv)/3)−1=0 Δ=[(4/3)(v−((4u^2 )/3))]^3 +[(1/2)(((16uv)/3)−1)]^2 Δ=((64)/(729))(3v−4u^2 )^3 +(1/(36))(16uv−3)^2 >0, say Q=(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) P=p^2 =((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) ⇒p=±(√(((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) )) ⇒x=(1/2){±(√(((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) ))±(√(((8u)/3)−(((√Δ)−(1/6)(16uv−3)))^(1/3) +(((√Δ)+(1/6)(16uv−3)))^(1/3) ∓(2/(√(((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) )))))} ⇒p=(1/4){±(√(((4a^2 )/3)+(((√Δ)−(1/6)(16a^2 b^2 −3)))^(1/3) −(((√Δ)+(1/6)(16a^2 b^2 −3)))^(1/3) ))±(√(((8a^2 )/3)−(((√Δ)−(1/6)(16a^2 b^2 −3)))^(1/3) +(((√Δ)+(1/6)(16a^2 b^2 −3)))^(1/3) ∓(2/(√(((4a^2 )/3)+(((√Δ)−(1/6)(16a^2 b^2 −3)))^(1/3) −(((√Δ)+(1/6)(16a^2 b^2 −3)))^(1/3) )))))}^2 with Δ=((64)/(729))(3b^2 −4a^4 )^3 +(1/(36))(16a^2 b^2 −3)^2](Q65906.png)
