Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 14543 by chux last updated on 02/Jun/17

An open box of area 486cm^2 .If the length is twice the breadth.Find the maximum volume of the box. hence,Show the volume is maximum.

$$\mathrm{An}\:\mathrm{open}\:\mathrm{box}\:\mathrm{of}\:\mathrm{area}\:\mathrm{486cm}^{\mathrm{2}} .\mathrm{If}\:\mathrm{the} \\ $$$$\mathrm{length}\:\mathrm{is}\:\mathrm{twice}\:\mathrm{the}\:\mathrm{breadth}.\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{maximum}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{box}. \\ $$$$\mathrm{hence},\mathrm{Show}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{is}\:\mathrm{maximum}. \\ $$

Commented by chux last updated on 02/Jun/17

please help

$$\mathrm{please}\:\mathrm{help} \\ $$

Answered by sandy_suhendra last updated on 22/Jun/17

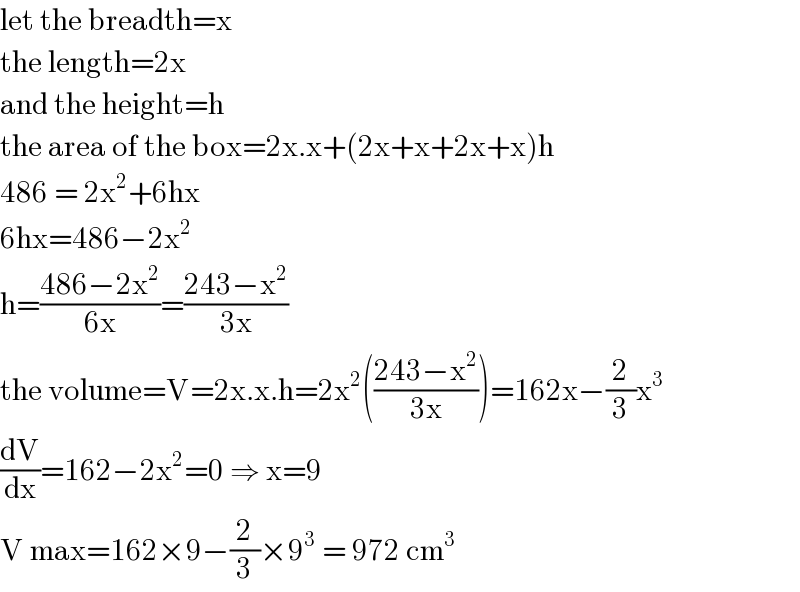
let the breadth=x the length=2x and the height=h the area of the box=2x.x+(2x+x+2x+x)h 486 = 2x^2 +6hx 6hx=486−2x^2 h=((486−2x^2 )/(6x))=((243−x^2 )/(3x)) the volume=V=2x.x.h=2x^2 (((243−x^2 )/(3x)))=162x−(2/3)x^3 (dV/dx)=162−2x^2 =0 ⇒ x=9 V max=162×9−(2/3)×9^3 = 972 cm^3

$$\mathrm{let}\:\mathrm{the}\:\mathrm{breadth}=\mathrm{x} \\ $$$$\mathrm{the}\:\mathrm{length}=\mathrm{2x} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{height}=\mathrm{h} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{box}=\mathrm{2x}.\mathrm{x}+\left(\mathrm{2x}+\mathrm{x}+\mathrm{2x}+\mathrm{x}\right)\mathrm{h} \\ $$$$\mathrm{486}\:=\:\mathrm{2x}^{\mathrm{2}} +\mathrm{6hx} \\ $$$$\mathrm{6hx}=\mathrm{486}−\mathrm{2x}^{\mathrm{2}} \\ $$$$\mathrm{h}=\frac{\mathrm{486}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{6x}}=\frac{\mathrm{243}−\mathrm{x}^{\mathrm{2}} }{\mathrm{3x}} \\ $$$$\mathrm{the}\:\mathrm{volume}=\mathrm{V}=\mathrm{2x}.\mathrm{x}.\mathrm{h}=\mathrm{2x}^{\mathrm{2}} \left(\frac{\mathrm{243}−\mathrm{x}^{\mathrm{2}} }{\mathrm{3x}}\right)=\mathrm{162x}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:\:\:\:\: \\ $$$$\frac{\mathrm{dV}}{\mathrm{dx}}=\mathrm{162}−\mathrm{2x}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:\mathrm{x}=\mathrm{9} \\ $$$$\mathrm{V}\:\mathrm{max}=\mathrm{162}×\mathrm{9}−\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{9}^{\mathrm{3}} \:=\:\mathrm{972}\:\mathrm{cm}^{\mathrm{3}} \\ $$

Answered by Tinkutara last updated on 02/Jun/17

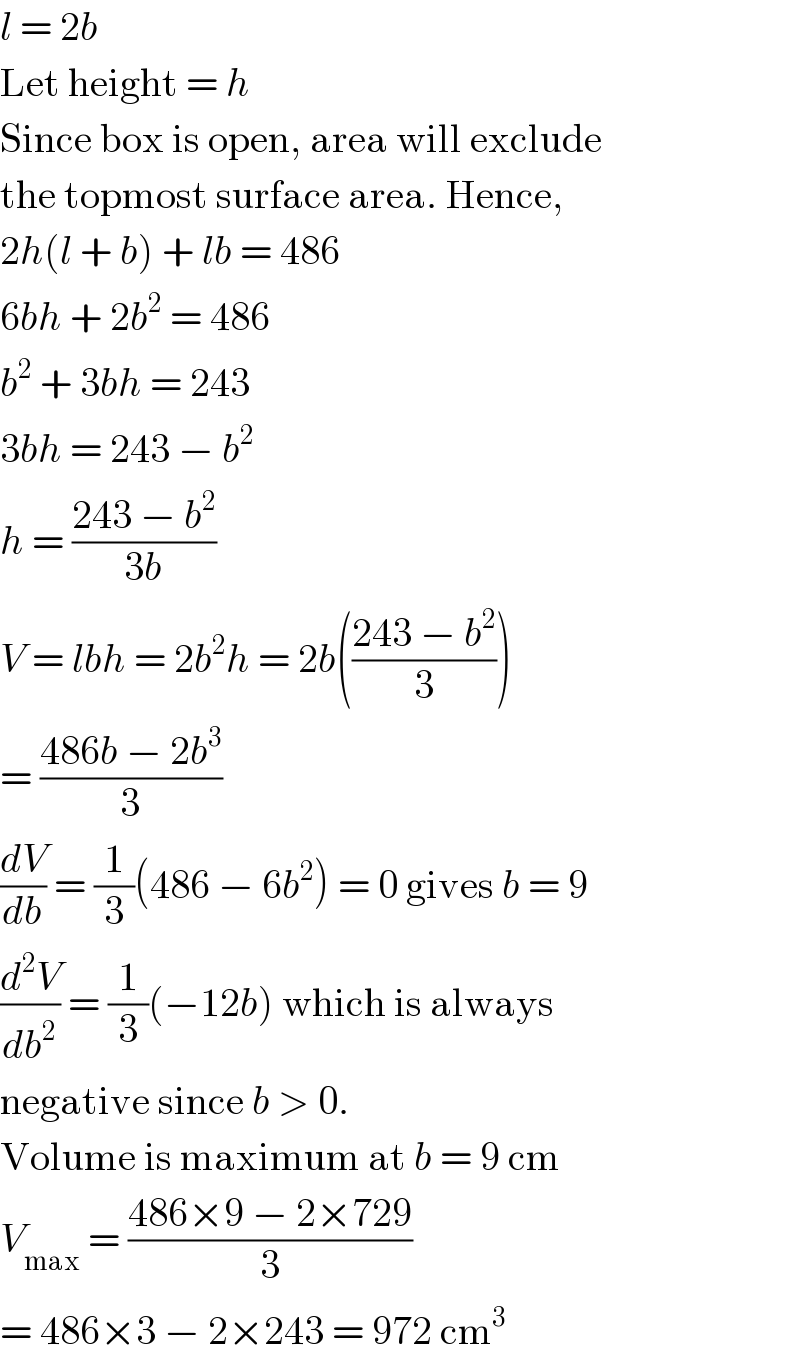
l = 2b Let height = h Since box is open, area will exclude the topmost surface area. Hence, 2h(l + b) + lb = 486 6bh + 2b^2 = 486 b^2 + 3bh = 243 3bh = 243 − b^2 h = ((243 − b^2 )/(3b)) V = lbh = 2b^2 h = 2b(((243 − b^2 )/3)) = ((486b − 2b^3 )/3) (dV/db) = (1/3)(486 − 6b^2 ) = 0 gives b = 9 (d^2 V/db^2 ) = (1/3)(−12b) which is always negative since b > 0. Volume is maximum at b = 9 cm V_(max) = ((486×9 − 2×729)/3) = 486×3 − 2×243 = 972 cm^3

$${l}\:=\:\mathrm{2}{b} \\ $$$$\mathrm{Let}\:\mathrm{height}\:=\:{h} \\ $$$$\mathrm{Since}\:\mathrm{box}\:\mathrm{is}\:\mathrm{open},\:\mathrm{area}\:\mathrm{will}\:\mathrm{exclude} \\ $$$$\mathrm{the}\:\mathrm{topmost}\:\mathrm{surface}\:\mathrm{area}.\:\mathrm{Hence}, \\ $$$$\mathrm{2}{h}\left({l}\:+\:{b}\right)\:+\:{lb}\:=\:\mathrm{486} \\ $$$$\mathrm{6}{bh}\:+\:\mathrm{2}{b}^{\mathrm{2}} \:=\:\mathrm{486} \\ $$$${b}^{\mathrm{2}} \:+\:\mathrm{3}{bh}\:=\:\mathrm{243} \\ $$$$\mathrm{3}{bh}\:=\:\mathrm{243}\:−\:{b}^{\mathrm{2}} \\ $$$${h}\:=\:\frac{\mathrm{243}\:−\:{b}^{\mathrm{2}} }{\mathrm{3}{b}} \\ $$$${V}\:=\:{lbh}\:=\:\mathrm{2}{b}^{\mathrm{2}} {h}\:=\:\mathrm{2}{b}\left(\frac{\mathrm{243}\:−\:{b}^{\mathrm{2}} }{\mathrm{3}}\right) \\ $$$$=\:\frac{\mathrm{486}{b}\:−\:\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\frac{{dV}}{{db}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{486}\:−\:\mathrm{6}{b}^{\mathrm{2}} \right)\:=\:\mathrm{0}\:\mathrm{gives}\:{b}\:=\:\mathrm{9} \\ $$$$\frac{{d}^{\mathrm{2}} {V}}{{db}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(−\mathrm{12}{b}\right)\:\mathrm{which}\:\mathrm{is}\:\mathrm{always} \\ $$$$\mathrm{negative}\:\mathrm{since}\:{b}\:>\:\mathrm{0}. \\ $$$$\mathrm{Volume}\:\mathrm{is}\:\mathrm{maximum}\:\mathrm{at}\:{b}\:=\:\mathrm{9}\:\mathrm{cm} \\ $$$${V}_{\mathrm{max}} \:=\:\frac{\mathrm{486}×\mathrm{9}\:−\:\mathrm{2}×\mathrm{729}}{\mathrm{3}} \\ $$$$=\:\mathrm{486}×\mathrm{3}\:−\:\mathrm{2}×\mathrm{243}\:=\:\mathrm{972}\:\mathrm{cm}^{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com