Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 14588 by tawa tawa last updated on 02/Jun/17

Determine the fourth roots of − 16, giving the results in the form a + jb.

$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{fourth}\:\mathrm{roots}\:\mathrm{of}\:\:\:−\:\mathrm{16},\:\:\:\mathrm{giving}\:\mathrm{the}\:\mathrm{results}\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}\:\:\mathrm{a}\:+\:\mathrm{jb}. \\ $$

Answered by mrW1 last updated on 03/Jun/17

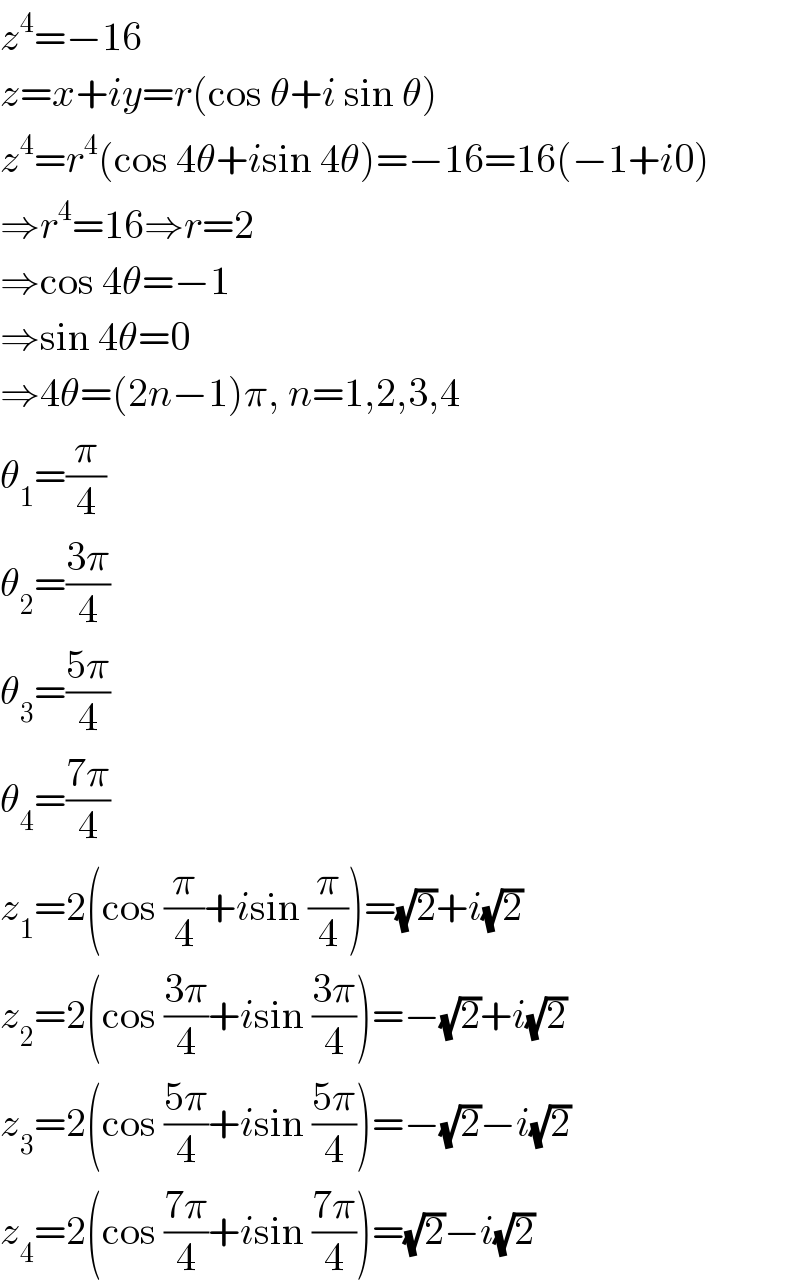
z^4 =−16 z=x+iy=r(cos θ+i sin θ) z^4 =r^4 (cos 4θ+isin 4θ)=−16=16(−1+i0) ⇒r^4 =16⇒r=2 ⇒cos 4θ=−1 ⇒sin 4θ=0 ⇒4θ=(2n−1)π, n=1,2,3,4 θ_1 =(π/4) θ_2 =((3π)/4) θ_3 =((5π)/4) θ_4 =((7π)/4) z_1 =2(cos (π/4)+isin (π/4))=(√2)+i(√2) z_2 =2(cos ((3π)/4)+isin ((3π)/4))=−(√2)+i(√2) z_3 =2(cos ((5π)/4)+isin ((5π)/4))=−(√2)−i(√2) z_4 =2(cos ((7π)/4)+isin ((7π)/4))=(√2)−i(√2)

$${z}^{\mathrm{4}} =−\mathrm{16} \\ $$$${z}={x}+{iy}={r}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right) \\ $$$${z}^{\mathrm{4}} ={r}^{\mathrm{4}} \left(\mathrm{cos}\:\mathrm{4}\theta+{i}\mathrm{sin}\:\mathrm{4}\theta\right)=−\mathrm{16}=\mathrm{16}\left(−\mathrm{1}+{i}\mathrm{0}\right) \\ $$$$\Rightarrow{r}^{\mathrm{4}} =\mathrm{16}\Rightarrow{r}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{4}\theta=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{4}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\theta=\left(\mathrm{2}{n}−\mathrm{1}\right)\pi,\:{n}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4} \\ $$$$\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{4}} \\ $$$$\theta_{\mathrm{2}} =\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\theta_{\mathrm{3}} =\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$$$\theta_{\mathrm{4}} =\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$${z}_{\mathrm{1}} =\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+{i}\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}+{i}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{2}} =\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}+{i}\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right)=−\sqrt{\mathrm{2}}+{i}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{3}} =\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{4}}+{i}\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{4}}\right)=−\sqrt{\mathrm{2}}−{i}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{4}} =\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{4}}+{i}\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}−{i}\sqrt{\mathrm{2}} \\ $$

Commented by tawa tawa last updated on 04/Jun/17

Wow, i really appreciate sir. God bless you.

$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Commented by RasheedSoomro last updated on 04/Jun/17

∈×cellent!

$$\in×\mathrm{cellent}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com