
Question and Answers Forum
Question Number 146157 by henderson last updated on 11/Jul/21
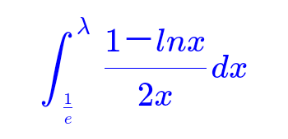
Answered by gsk2684 last updated on 11/Jul/21
![∫_(1/e) ^λ (1/2)(1−ln x)((d(1−ln x))/(−1)) −(1/2)[(((1−ln x)^2 )/2)]_(1/e) ^λ −(1/4)[(1−ln λ)^2 −(1−ln (1/e))^2 ] −(1/4)[(1−ln λ)^2 −4]](Q146159.png)
Answered by hknkrc46 last updated on 11/Jul/21
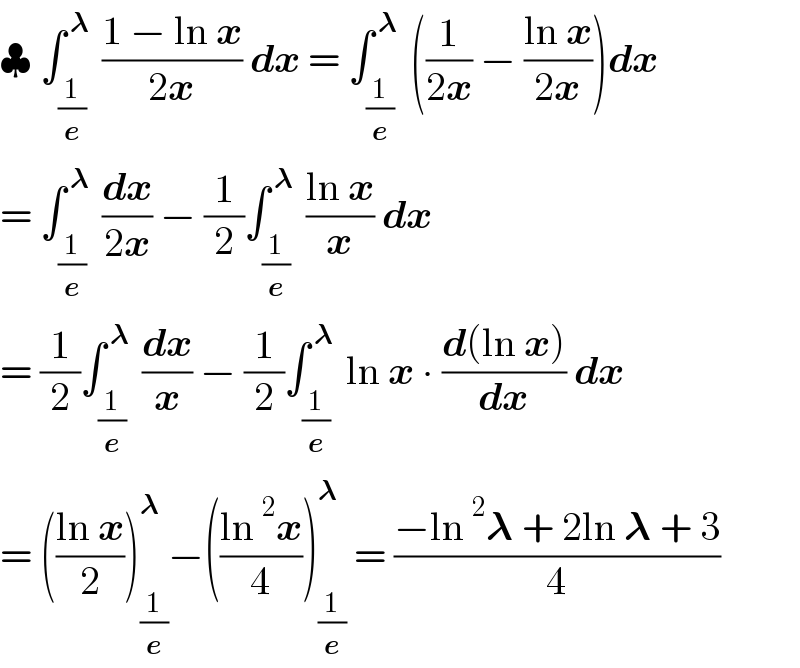
Answered by mathmax by abdo last updated on 11/Jul/21
![A_λ =∫_(1/e) ^λ ((1−logx)/(2x))dx changement logx=t give x=e^t ⇒ A_λ =∫_(−1) ^(logλ) ((1−t)/(2e^t ))e^t dt =∫_(−1) ^(logλ) (1−t)dt=(1/2)[t−(t^2 /2)]_(−1) ^(logλ) =(1/2)(logλ−((log^2 λ)/2) +1+(1/2))=(1/2)logλ−(1/4)log^2 λ+(3/4)](Q146163.png)
| ||
Question and Answers Forum | ||
Question Number 146157 by henderson last updated on 11/Jul/21 | ||
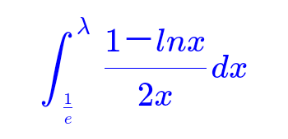 | ||
Answered by gsk2684 last updated on 11/Jul/21 | ||
![∫_(1/e) ^λ (1/2)(1−ln x)((d(1−ln x))/(−1)) −(1/2)[(((1−ln x)^2 )/2)]_(1/e) ^λ −(1/4)[(1−ln λ)^2 −(1−ln (1/e))^2 ] −(1/4)[(1−ln λ)^2 −4]](Q146159.png) | ||
| ||
Answered by hknkrc46 last updated on 11/Jul/21 | ||
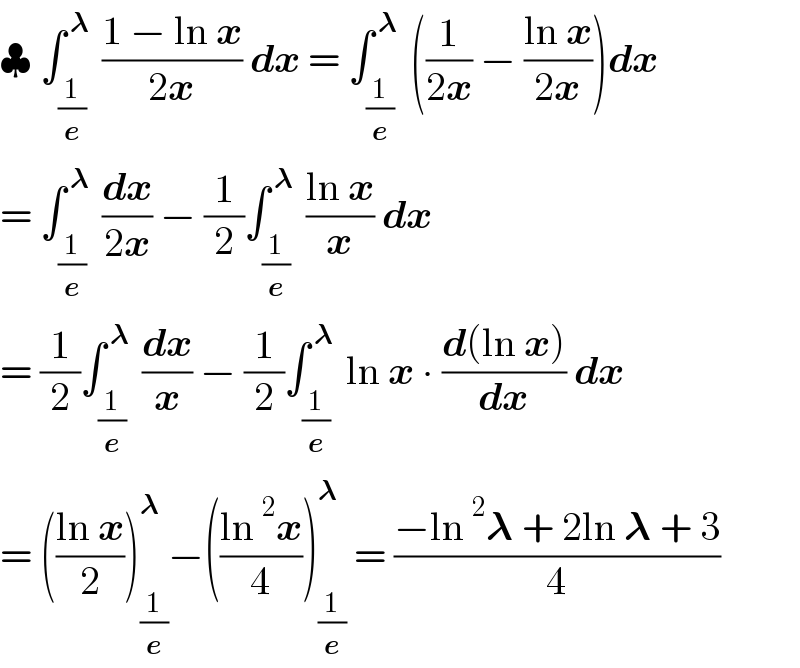 | ||
| ||
Answered by mathmax by abdo last updated on 11/Jul/21 | ||
![A_λ =∫_(1/e) ^λ ((1−logx)/(2x))dx changement logx=t give x=e^t ⇒ A_λ =∫_(−1) ^(logλ) ((1−t)/(2e^t ))e^t dt =∫_(−1) ^(logλ) (1−t)dt=(1/2)[t−(t^2 /2)]_(−1) ^(logλ) =(1/2)(logλ−((log^2 λ)/2) +1+(1/2))=(1/2)logλ−(1/4)log^2 λ+(3/4)](Q146163.png) | ||
| ||