Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 146181 by mnjuly1970 last updated on 11/Jul/21

$$$$$$\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^n(n+1)(n+2)}=?$$

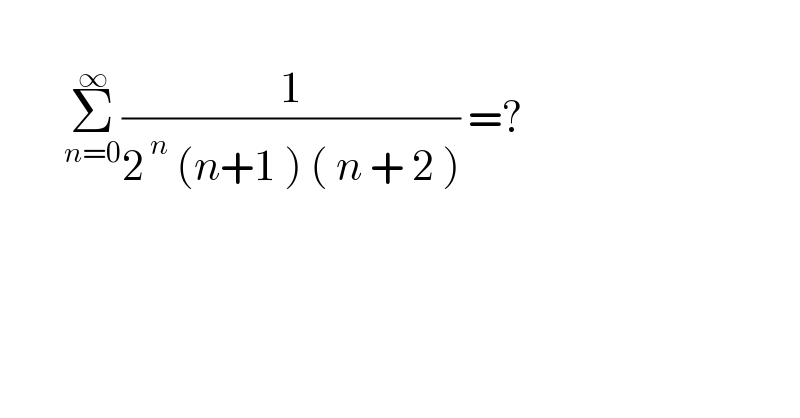
Answered by Olaf_Thorendsen last updated on 11/Jul/21

$$\mathrm{S}=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^n(n+1)(n+2)}$$$$\mathrm{S}=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^n}(\frac{1}{n+1}-\frac{1}{n+2})$$$$\frac{1}{1-x}=\mathrm{\Sigma }{x}^n,\mid x\mid <1$$$$-\ln \mid 1-x\mid =\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{x^{n+1}}{n+1}$$$$\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^n}.\frac{1}{n+1}=2\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}^{n+1}}{n+1}=-2\ln \mid 1-\frac{1}{2}\mid =2\ln 2$$$$\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^n}.\frac{1}{n+2}=4\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}^{n+2}}{n+2}=4\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}^{n+1}}{n+1}-2=-4\ln \mid 1-\frac{1}{2}\mid -2=4\ln 2-2$$$$\mathrm{S}=2\ln 2-(4\ln 2-2)=2-2\ln 2$$

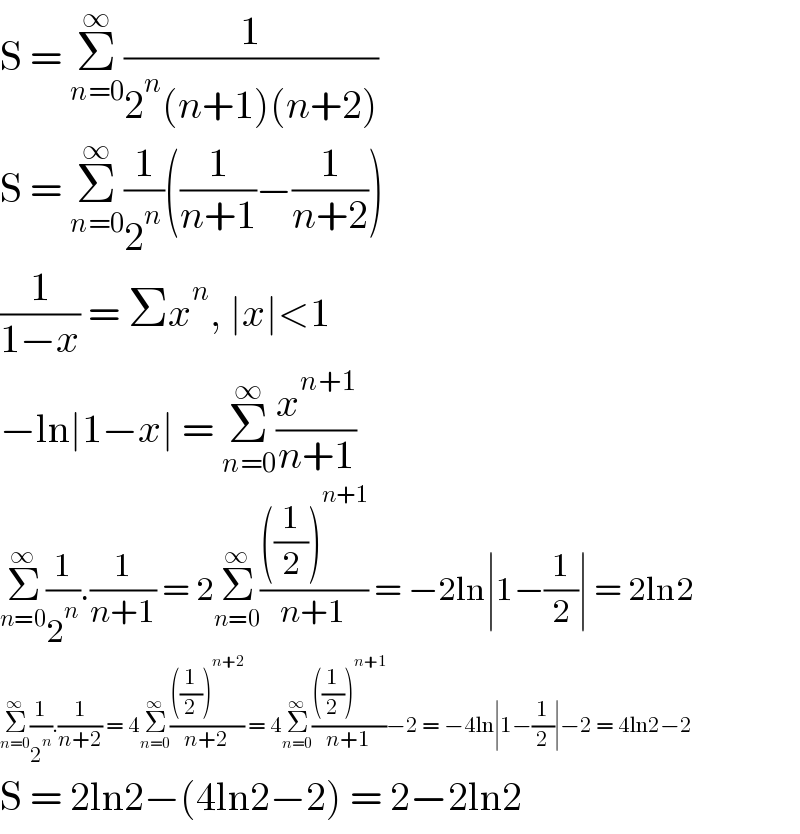
Answered by Ar Brandon last updated on 11/Jul/21

$$\mathrm{S}\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}\frac{{\mathrm{x}}^{\mathrm{n}+2}}{(\mathrm{n}+1)(\mathrm{n}+2)}\Rightarrow {\mathrm{S}}^{\prime }\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}\frac{{\mathrm{x}}^{\mathrm{n}+1}}{\mathrm{n}+1}\Rightarrow {\mathrm{S}}^{″}\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}{\mathrm{x}}^{\mathrm{n}}=\frac{1}{1-\mathrm{x}}$$$$\Rightarrow {\mathrm{S}}^{\prime }\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}{\underset{0}{\int }}^{\mathrm{x}}{\mathrm{x}}^{\mathrm{n}}\mathrm{dx}={\int }_0^{\mathrm{x}}\frac{\mathrm{dx}}{1-\mathrm{x}}\Rightarrow {\mathrm{S}}^{\prime }\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}\frac{{\mathrm{x}}^{\mathrm{n}+1}}{\mathrm{n}+1}=\ln \left(\frac{1}{1-\mathrm{x}}\right)$$$$\Rightarrow \mathrm{S}\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}{\int }_0^{\mathrm{x}}\frac{{\mathrm{x}}^{\mathrm{n}+1}}{\mathrm{n}+1}\mathrm{dx}={\int }_0^{\mathrm{x}}\ln \left(\frac{1}{1-\mathrm{x}}\right)\mathrm{dx}$$$$\Rightarrow \mathrm{S}\left(\mathrm{x}\right)=\sum _{\mathrm{n}⩾0}\frac{{\mathrm{x}}^{\mathrm{n}+2}}{(\mathrm{n}+1)(\mathrm{n}+2)}={[(1-\mathrm{x})\ln (1-\mathrm{x})-(1-\mathrm{x})]}_0^{\mathrm{x}}$$$$\Rightarrow \mathrm{S}\left(\mathrm{x}\right)=(1-\mathrm{x})\ln (1-\mathrm{x})-(1-\mathrm{x})+1=(1-\mathrm{x})\ln (1-\mathrm{x})+\mathrm{x}$$$$\sum _{\mathrm{n}⩾0}\frac{1}{2^{\mathrm{n}}(\mathrm{n}+1)(\mathrm{n}+2)}=4\mathrm{S}\left(\frac{1}{2}\right)=4(\frac{1}{2}\ln \left(\frac{1}{2}\right)+\frac{1}{2})=2-2\ln 2$$

Answered by qaz last updated on 11/Jul/21

$$\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^{\mathrm{n}}(\mathrm{n}+1)(\mathrm{n}+2)}$$$$=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^{\mathrm{n}}}(\frac{1}{\mathrm{n}+1}-\frac{1}{\mathrm{n}+2})$$$$=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{1}{2^{\mathrm{n}}}{\int }_0^1({\mathrm{x}}^{\mathrm{n}}-{\mathrm{x}}^{\mathrm{n}+1})\mathrm{dx}$$$$={\int }_0^1\frac{1-\mathrm{x}}{1-\frac{\mathrm{x}}{2}}\mathrm{dx}$$$$=2{\int }_0^1(1-\frac{1}{2-\mathrm{x}})\mathrm{dx}$$$$=2(\mathrm{x}+\ln (2-\mathrm{x})){\mid }_0^1$$$$=2-2\ln 2$$

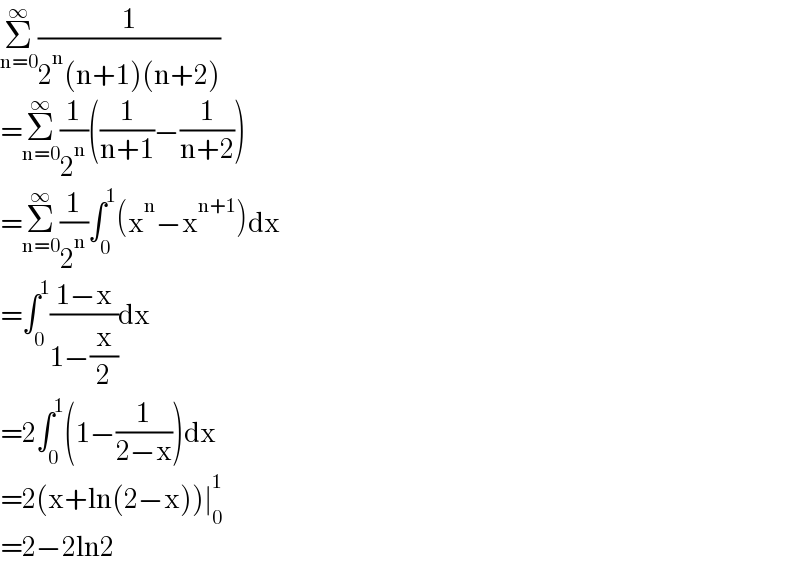
Answered by mathmax by abdo last updated on 11/Jul/21

$$\mathrm{S}=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{1}{(\mathrm{n}+1)(\mathrm{n}+2)2^{\mathrm{n}}}\mathrm{let}\mathrm{f}\left(\mathrm{x}\right)=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{(\mathrm{n}+1)(\mathrm{n}+2)}\Rightarrow$$$$\Rightarrow \mathrm{f}\left(\mathrm{x}\right)=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}(\frac{1}{\mathrm{n}+1}-\frac{1}{\mathrm{n}+2}){\mathrm{x}}^{\mathrm{n}}=\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}+1}-\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}+2}$$$$\mathrm{we}\mathrm{have}\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}+1}=\sum _{\mathrm{n}=1}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}-1}}{\mathrm{n}}=\frac{1}{\mathrm{x}}\sum _{\mathrm{n}=1}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}}=-\frac{1}{\mathrm{x}}\log (1-\mathrm{x})$$$$\sum _{\mathrm{n}=0}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}+2}=\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}-2}}{\mathrm{n}}=\frac{1}{{\mathrm{x}}^2}\sum _{\mathrm{n}=2}^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}}=\frac{1}{{\mathrm{x}}^2}(-\log (1-\mathrm{x})-\mathrm{x})\Rightarrow$$$$\mathrm{f}\left(\mathrm{x}\right)=-\frac{1}{\mathrm{x}}\log (1-\mathrm{x})+\frac{1}{{\mathrm{x}}^2}(\mathrm{x}+\log (1-\mathrm{x}))$$$$=\frac{1}{\mathrm{x}}+(\frac{1}{{\mathrm{x}}^2}-\frac{1}{\mathrm{x}})\log (1-\mathrm{x})$$$$\mathrm{S}=\mathrm{f}\left(\frac{1}{2}\right)=2+(4-2)\log \left(\frac{1}{2}\right)=2-2\log \left(2\right)$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com