Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 146212 by puissant last updated on 12/Jul/21

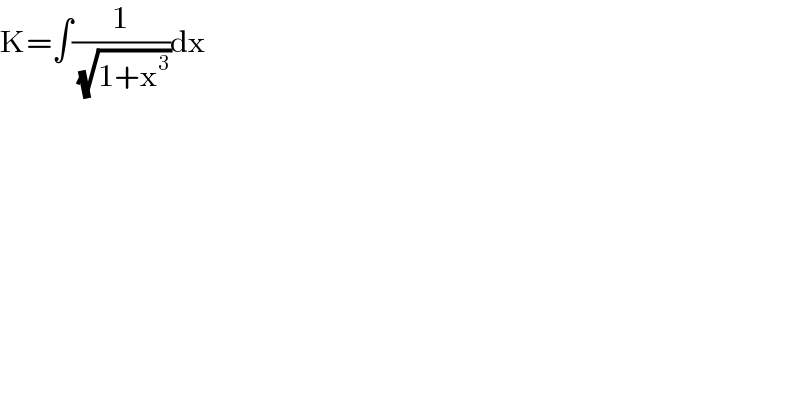
K=∫(1/( (√(1+x^3 ))))dx

$$\mathrm{K}=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }}\mathrm{dx} \\ $$

Answered by Ar Brandon last updated on 12/Jul/21

I=∫(dx/( (√(1+x^3 ))))=∫(dx/( (√(1+(x^(3/2) )^2 )))), u=x^(3/2) ⇒du=(3/2)x^(1/2) dx=(3/2)u^(1/3) dx =(2/3)∫(u^(−1/3) /( (√(1+u^2 ))))du, u=sinhϑ⇒du=coshϑdϑ =(2/3)∫(((sinhϑ)^(−1/3) )/(coshϑ))∙coshϑdϑ=(2/3)∫(sinhϑ)^(−1/3) dϑ =x _2 F_1 ((1/3); (1/2); (4/3); −x^3 ) , Hypergeome^� trique. ∫_0 ^∞ (dx/( (√(1+x^3 )))), u=x^3 ⇒(1/3)u^(−(2/3)) du=dx =(1/3)∫_0 ^∞ (u^(−(2/3)) /( (√(1+u))))du=(1/3)β((1/3), (1/6))=((Γ((1/3))Γ((1/6)))/(3Γ((1/2))))=((Γ((1/3))Γ((1/6)))/(3(√π))) ≈2.80436421

$$\mathrm{I}=\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }}=\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\left(\mathrm{x}^{\mathrm{3}/\mathrm{2}} \right)^{\mathrm{2}} }},\:\mathrm{u}=\mathrm{x}^{\mathrm{3}/\mathrm{2}} \Rightarrow\mathrm{du}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{1}/\mathrm{2}} \mathrm{dx}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{u}^{\mathrm{1}/\mathrm{3}} \mathrm{dx} \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{u}^{−\mathrm{1}/\mathrm{3}} }{\:\sqrt{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}\mathrm{du},\:\mathrm{u}=\mathrm{sinh}\vartheta\Rightarrow\mathrm{du}=\mathrm{cosh}\vartheta\mathrm{d}\vartheta \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\left(\mathrm{sinh}\vartheta\right)^{−\mathrm{1}/\mathrm{3}} }{\mathrm{cosh}\vartheta}\centerdot\mathrm{cosh}\vartheta\mathrm{d}\vartheta=\frac{\mathrm{2}}{\mathrm{3}}\int\left(\mathrm{sinh}\vartheta\right)^{−\mathrm{1}/\mathrm{3}} \mathrm{d}\vartheta \\ $$$$\:\:=\mathrm{x}\underset{\mathrm{2}} {\:}{F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}};\:\frac{\mathrm{1}}{\mathrm{2}};\:\frac{\mathrm{4}}{\mathrm{3}};\:−\mathrm{x}^{\mathrm{3}} \right)\:,\:\mathrm{Hypergeom}\acute {\mathrm{e}trique}. \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }},\:\mathrm{u}=\mathrm{x}^{\mathrm{3}} \Rightarrow\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}^{−\frac{\mathrm{2}}{\mathrm{3}}} \mathrm{du}=\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\frac{\mathrm{2}}{\mathrm{3}}} }{\:\sqrt{\mathrm{1}+\mathrm{u}}}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{3}}\beta\left(\frac{\mathrm{1}}{\mathrm{3}},\:\frac{\mathrm{1}}{\mathrm{6}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}{\mathrm{3}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}{\mathrm{3}\sqrt{\pi}} \\ $$$$\approx\mathrm{2}.\mathrm{80436421} \\ $$

Commented by puissant last updated on 12/Jul/21

merci mais on ne peut faire ca avec le theoreme des residus..??

$$\mathrm{merci}\:\mathrm{mais}\:\mathrm{on}\:\mathrm{ne}\:\:\mathrm{peut}\:\mathrm{faire}\:\mathrm{ca}\:\mathrm{avec}\:\mathrm{le}\:\mathrm{theoreme} \\ $$$$\mathrm{des}\:\mathrm{residus}..?? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com