Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 146361 by gsk2684 last updated on 13/Jul/21

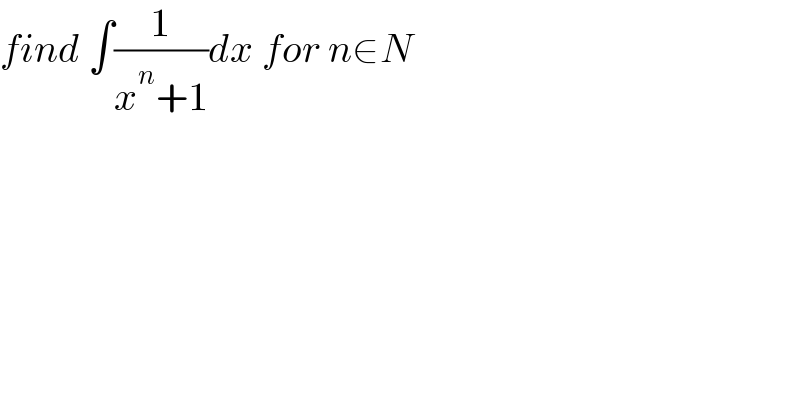
find ∫(1/(x^n +1))dx for n∈N

$${find}\:\int\frac{\mathrm{1}}{{x}^{{n}} +\mathrm{1}}{dx}\:{for}\:{n}\in{N} \\ $$

Answered by mathmax by abdo last updated on 13/Jul/21

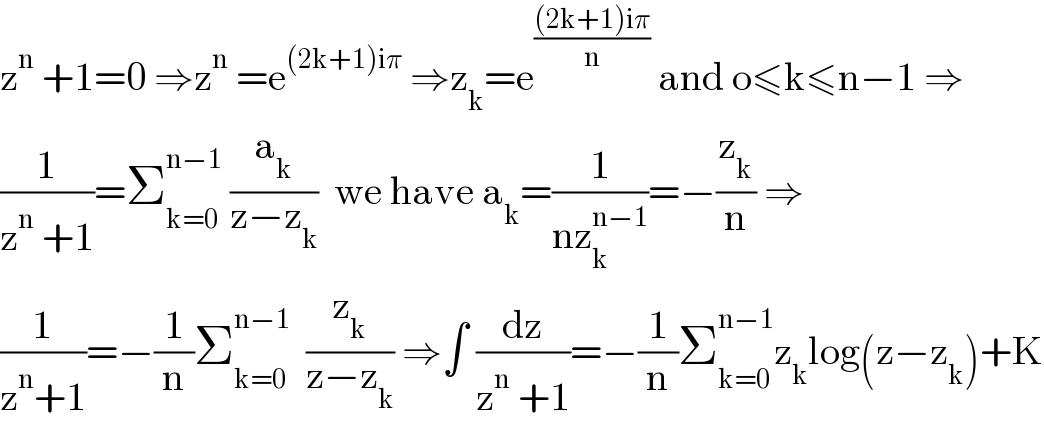
z^n +1=0 ⇒z^n =e^((2k+1)iπ) ⇒z_k =e^(((2k+1)iπ)/n) and o≤k≤n−1 ⇒ (1/(z^n +1))=Σ_(k=0) ^(n−1) (a_k /(z−z_k )) we have a_k =(1/(nz_k ^(n−1) ))=−(z_k /n) ⇒ (1/(z^n +1))=−(1/n)Σ_(k=0) ^(n−1) (z_k /(z−z_k )) ⇒∫ (dz/(z^n +1))=−(1/n)Σ_(k=0) ^(n−1) z_k log(z−z_k )+K

$$\mathrm{z}^{\mathrm{n}} \:+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{z}^{\mathrm{n}} \:=\mathrm{e}^{\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}\pi} \:\Rightarrow\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\frac{\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}\pi}{\mathrm{n}}} \:\mathrm{and}\:\mathrm{o}\leqslant\mathrm{k}\leqslant\mathrm{n}−\mathrm{1}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} \:+\mathrm{1}}=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{nz}_{\mathrm{k}} ^{\mathrm{n}−\mathrm{1}} }=−\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} +\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\:\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\Rightarrow\int\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{n}} \:+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \mathrm{z}_{\mathrm{k}} \mathrm{log}\left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)+\mathrm{K} \\ $$

Commented by gsk2684 last updated on 13/Jul/21

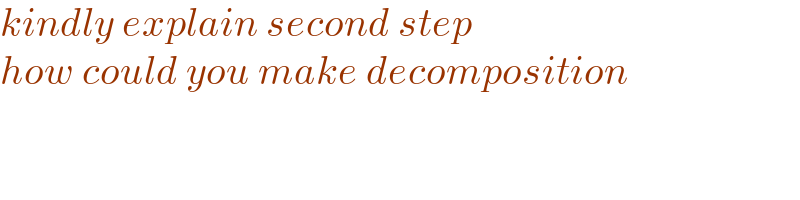
kindly explain second step how could you make decomposition

$${kindly}\:{explain}\:{second}\:{step}\: \\ $$$${how}\:{could}\:{you}\:{make}\:{decomposition} \\ $$

Commented by mathmax by abdo last updated on 13/Jul/21

if ((p(x))/(q(x)))=Σ (a_i /(x−x_i )) with degp<degq and x_i simples roots ⇒a_i =((p(x_i ))/(q^′ (x_i )))

$$\mathrm{if}\:\frac{\mathrm{p}\left(\mathrm{x}\right)}{\mathrm{q}\left(\mathrm{x}\right)}=\Sigma\:\frac{\mathrm{a}_{\mathrm{i}} }{\mathrm{x}−\mathrm{x}_{\mathrm{i}} }\:\:\mathrm{with}\:\mathrm{degp}<\mathrm{degq}\:\:\:\mathrm{and}\:\mathrm{x}_{\mathrm{i}} \mathrm{simples}\:\mathrm{roots} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{i}} =\frac{\mathrm{p}\left(\mathrm{x}_{\mathrm{i}} \right)}{\mathrm{q}^{'} \left(\mathrm{x}_{\mathrm{i}} \right)} \\ $$

Commented by gsk2684 last updated on 14/Jul/21

thank you

$${thank}\:{you}\: \\ $$

Answered by Snail last updated on 13/Jul/21

∫((x^(n−1) dx)/(x^(n−1) (x^n +1))) =(1/n)∫(( dt)/(1+(1/t))) where x^n =t(let) =(1/n)[∫dt−∫(dt/(t+1))] =(1/n)[t−ln(t+1)+C] =(1/n)[x^n −ln(x^n +1)]+C

$$\int\frac{{x}^{{n}−\mathrm{1}} {dx}}{{x}^{{n}−\mathrm{1}} \left({x}^{{n}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{n}}\int\frac{\:{dt}}{\mathrm{1}+\frac{\mathrm{1}}{{t}}}\:\:\:\:\:{where}\:\:{x}^{{n}} ={t}\left({let}\right) \\ $$$$=\frac{\mathrm{1}}{{n}}\left[\int{dt}−\int\frac{{dt}}{{t}+\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{1}}{{n}}\left[{t}−{ln}\left({t}+\mathrm{1}\right)+{C}\right] \\ $$$$=\frac{\mathrm{1}}{{n}}\left[{x}^{{n}} −{ln}\left({x}^{{n}} +\mathrm{1}\right)\right]+{C} \\ $$

Commented by gsk2684 last updated on 14/Jul/21

how could you write second step? please

$${how}\:{could}\:{you}\:{write}\:{second}\:{step}?\:{please} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com