
Question and Answers Forum
Question Number 146371 by lapache last updated on 13/Jul/21
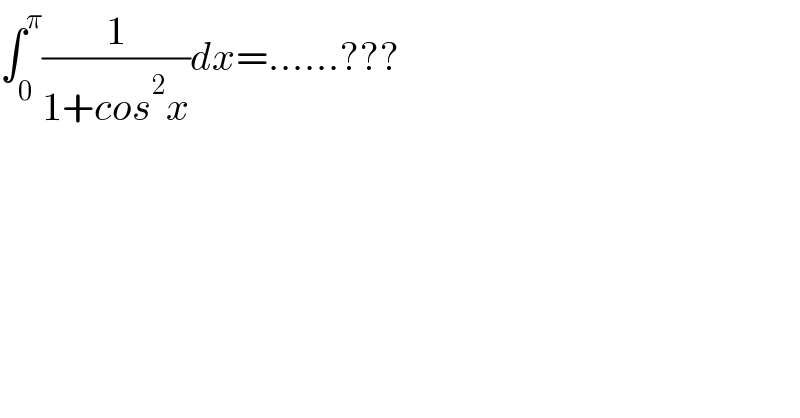
Answered by gsk2684 last updated on 13/Jul/21
![let I=∫_0 ^Π (1/(1+cos^2 x)) dx (1) f(Π−x)=(1/(1+cos^2 (Π−x))) =(1/(1+cos^2 x))=f(x) (1)⇒I=2∫_0 ^(Π/2) (1/(1+cos^2 x))dx ⇒I=2∫_0 ^(Π/2) (1/(sec^2 x+1)) sec^2 x dx ⇒I=2∫_0 ^(Π/2) (1/(1+tan^2 x+1)) sec^2 x dx ⇒I=2∫_0 ^(Π/2) (1/(tan^2 x+((√2))^2 )) d(tan x) ⇒I=2[(1/( (√2)))tan^(−1) (((tan x)/( (√2))))]_0 ^(Π/2) ⇒I=(√2)[(Π/2)−0]=(Π/( (√2)))](Q146372.png)
Answered by Ar Brandon last updated on 13/Jul/21
![I=∫_0 ^π (dx/(1+cos^2 x))=2∫_0 ^(π/2) ((sec^2 x)/(sec^2 x+1))dx =2∫_0 ^(π/2) ((d(tanx))/(2+tan^2 x))=(2/( (√2)))[arctan(((tanx)/( (√2))))]_0 ^(π/2) =(π/( (√2)))](Q146406.png)
Answered by mathmax by abdo last updated on 13/Jul/21

| ||
Question and Answers Forum | ||
Question Number 146371 by lapache last updated on 13/Jul/21 | ||
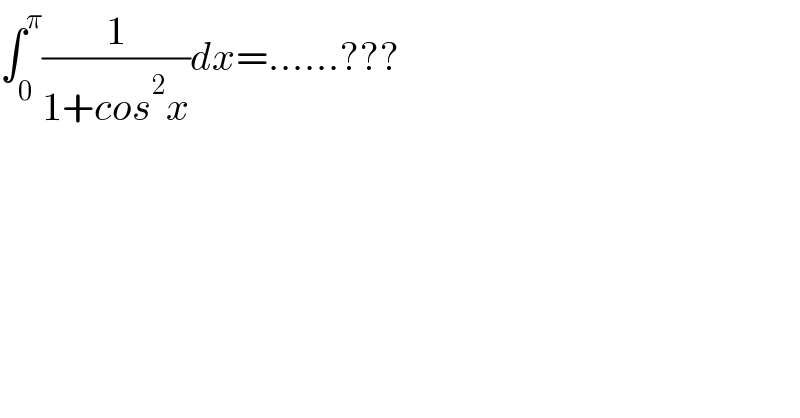 | ||
Answered by gsk2684 last updated on 13/Jul/21 | ||
![let I=∫_0 ^Π (1/(1+cos^2 x)) dx (1) f(Π−x)=(1/(1+cos^2 (Π−x))) =(1/(1+cos^2 x))=f(x) (1)⇒I=2∫_0 ^(Π/2) (1/(1+cos^2 x))dx ⇒I=2∫_0 ^(Π/2) (1/(sec^2 x+1)) sec^2 x dx ⇒I=2∫_0 ^(Π/2) (1/(1+tan^2 x+1)) sec^2 x dx ⇒I=2∫_0 ^(Π/2) (1/(tan^2 x+((√2))^2 )) d(tan x) ⇒I=2[(1/( (√2)))tan^(−1) (((tan x)/( (√2))))]_0 ^(Π/2) ⇒I=(√2)[(Π/2)−0]=(Π/( (√2)))](Q146372.png) | ||
| ||
Answered by Ar Brandon last updated on 13/Jul/21 | ||
![I=∫_0 ^π (dx/(1+cos^2 x))=2∫_0 ^(π/2) ((sec^2 x)/(sec^2 x+1))dx =2∫_0 ^(π/2) ((d(tanx))/(2+tan^2 x))=(2/( (√2)))[arctan(((tanx)/( (√2))))]_0 ^(π/2) =(π/( (√2)))](Q146406.png) | ||
| ||
Answered by mathmax by abdo last updated on 13/Jul/21 | ||
 | ||
| ||