
Question Number 146386 by mathdanisur last updated on 13/Jul/21
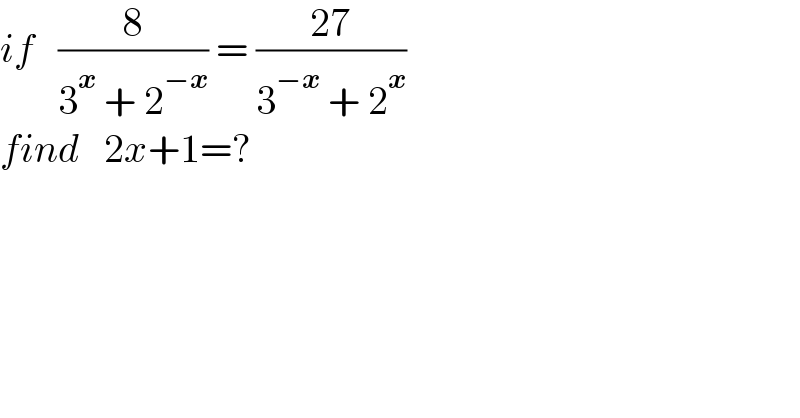
$${if}\:\:\:\frac{\mathrm{8}}{\mathrm{3}^{\boldsymbol{{x}}} \:+\:\mathrm{2}^{−\boldsymbol{{x}}} }\:=\:\frac{\mathrm{27}}{\mathrm{3}^{−\boldsymbol{{x}}} \:+\:\mathrm{2}^{\boldsymbol{{x}}} } \\ $$$${find}\:\:\:\mathrm{2}{x}+\mathrm{1}=? \\ $$
Answered by iloveisrael last updated on 13/Jul/21
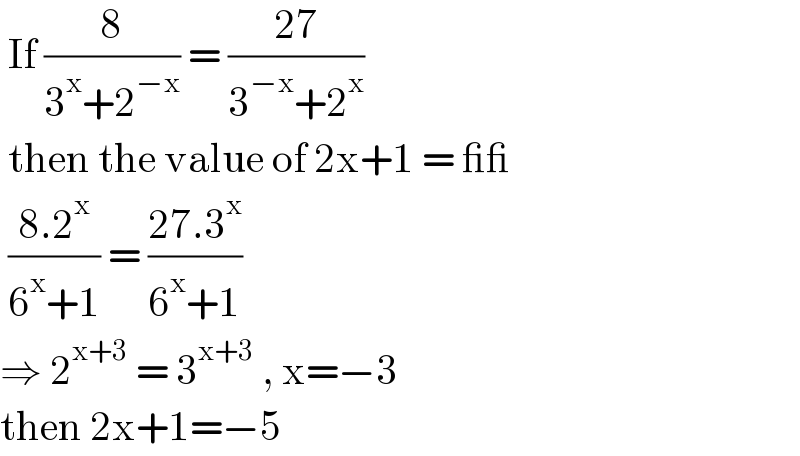
$$\:\mathrm{If}\:\frac{\mathrm{8}}{\mathrm{3}^{\mathrm{x}} +\mathrm{2}^{−\mathrm{x}} }\:=\:\frac{\mathrm{27}}{\mathrm{3}^{−\mathrm{x}} +\mathrm{2}^{\mathrm{x}} }\: \\ $$$$\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{2x}+\mathrm{1}\:=\:\_\_ \\ $$$$\:\frac{\mathrm{8}.\mathrm{2}^{\mathrm{x}} }{\mathrm{6}^{\mathrm{x}} +\mathrm{1}}\:=\:\frac{\mathrm{27}.\mathrm{3}^{\mathrm{x}} }{\mathrm{6}^{\mathrm{x}} +\mathrm{1}}\: \\ $$$$\Rightarrow\:\mathrm{2}^{\mathrm{x}+\mathrm{3}} \:=\:\mathrm{3}^{\mathrm{x}+\mathrm{3}} \:,\:\mathrm{x}=−\mathrm{3} \\ $$$$\mathrm{then}\:\mathrm{2x}+\mathrm{1}=−\mathrm{5}\: \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by Rasheed.Sindhi last updated on 13/Jul/21
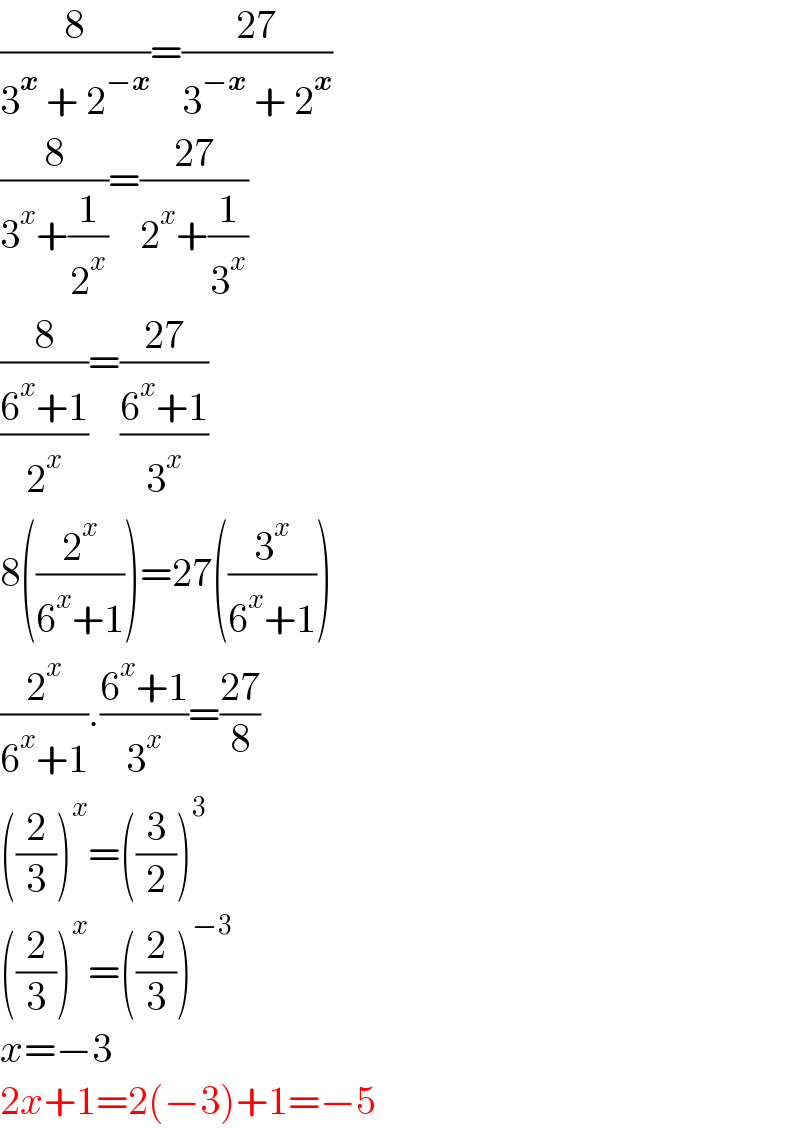
$$\frac{\mathrm{8}}{\mathrm{3}^{\boldsymbol{{x}}} \:+\:\mathrm{2}^{−\boldsymbol{{x}}} }=\frac{\mathrm{27}}{\mathrm{3}^{−\boldsymbol{{x}}} \:+\:\mathrm{2}^{\boldsymbol{{x}}} } \\ $$$$\frac{\mathrm{8}}{\mathrm{3}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}^{{x}} }}=\frac{\mathrm{27}}{\mathrm{2}^{{x}} +\frac{\mathrm{1}}{\mathrm{3}^{{x}} }} \\ $$$$\frac{\mathrm{8}}{\frac{\mathrm{6}^{{x}} +\mathrm{1}}{\mathrm{2}^{{x}} }}=\frac{\mathrm{27}}{\frac{\mathrm{6}^{{x}} +\mathrm{1}}{\mathrm{3}^{{x}} }} \\ $$$$\mathrm{8}\left(\frac{\mathrm{2}^{{x}} }{\mathrm{6}^{{x}} +\mathrm{1}}\right)=\mathrm{27}\left(\frac{\mathrm{3}^{{x}} }{\mathrm{6}^{{x}} +\mathrm{1}}\right) \\ $$$$\frac{\mathrm{2}^{{x}} }{\mathrm{6}^{{x}} +\mathrm{1}}.\frac{\mathrm{6}^{{x}} +\mathrm{1}}{\mathrm{3}^{{x}} }=\frac{\mathrm{27}}{\mathrm{8}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} =\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{3}} \\ $$$${x}=−\mathrm{3} \\ $$$$\mathrm{2}{x}+\mathrm{1}=\mathrm{2}\left(−\mathrm{3}\right)+\mathrm{1}=−\mathrm{5} \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
