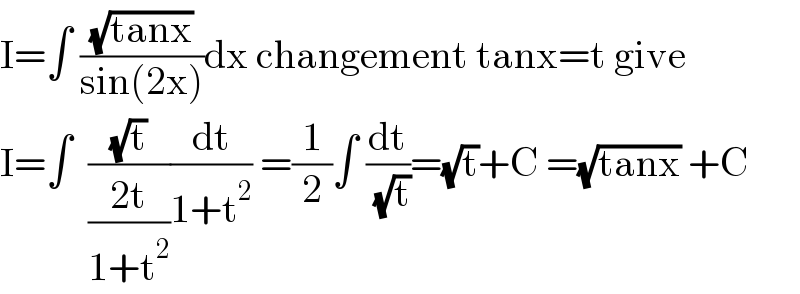Question and Answers Forum
Question Number 146597 by iloveisrael last updated on 14/Jul/21
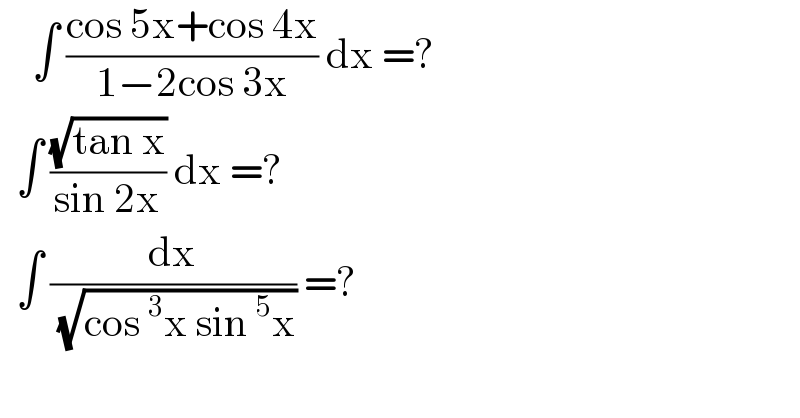
Answered by gsk2684 last updated on 14/Jul/21
![∫((cos 5x+cos 4x)/(1−2cos 3x))dx ∫ ((2cos ((5x+4x)/2)cos ((5x−4x)/2))/(1−2(2cos^2 ((3x)/2)−1))) dx 2∫((cos 3(((3x)/2))cos (x/2))/(1−4cos^2 ((3x)/2)+2))dx 2∫(([4cos^3 (((3x)/2))−3cos(((3x)/2))] cos (x/2))/(3−4cos^2 ((3x)/2)))dx 2∫(([4cos^2 (((3x)/2))−3]cos ((3x)/2) cos (x/2))/(3−4cos^2 ((3x)/2)))dx −∫2cos ((3x)/2)cos (x/2)dx −∫(cos (((3x)/2)+(x/2))+cos (((3x)/2)−(x/2)))dx −∫(cos 2x+cos x)dx −(((sin 2x)/2)+sin x)+c](Q146604.png)
Answered by gsk2684 last updated on 14/Jul/21
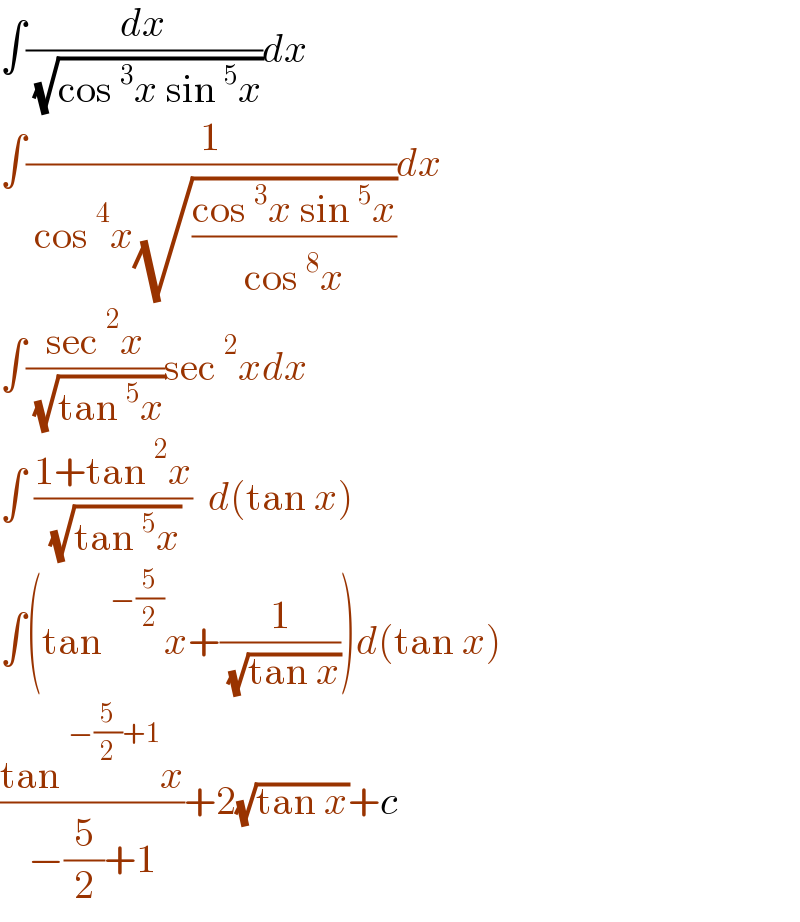
Answered by gsk2684 last updated on 14/Jul/21
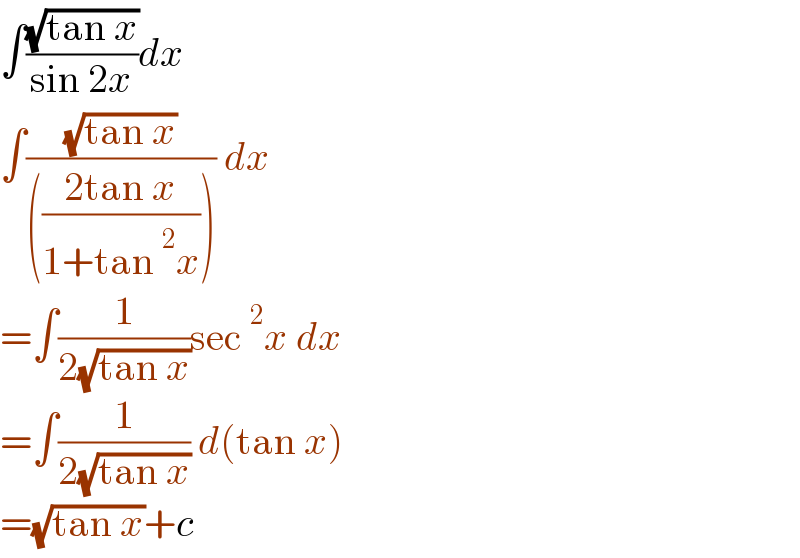
Answered by puissant last updated on 14/Jul/21
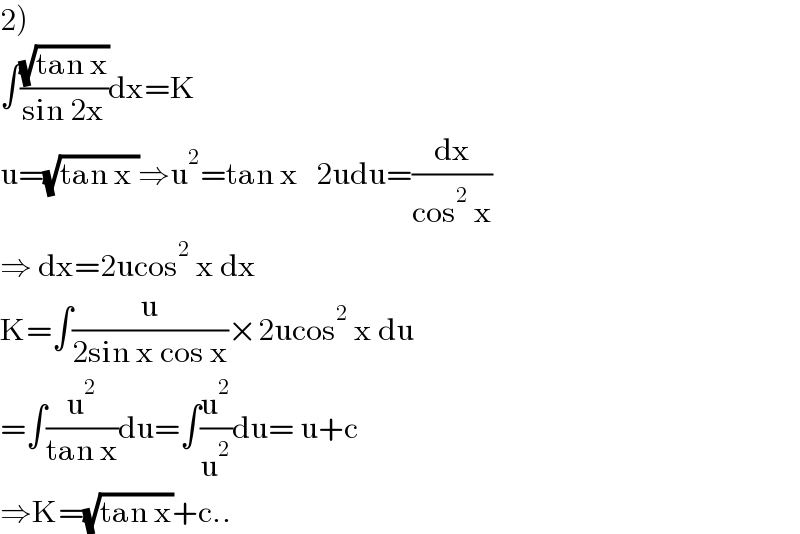
Answered by mathmax by abdo last updated on 14/Jul/21