
Question and Answers Forum
Question Number 146835 by mathmax by abdo last updated on 16/Jul/21
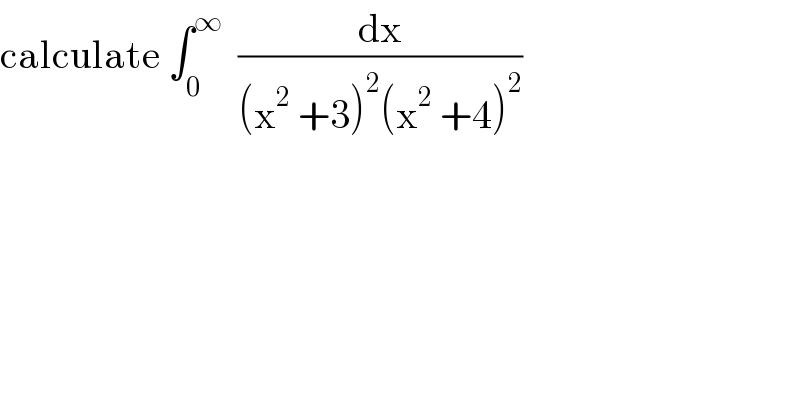
Answered by mathmax by abdo last updated on 16/Jul/21

Answered by Olaf_Thorendsen last updated on 16/Jul/21
![f(a,b) = ∫_0 ^∞ (dx/((x^2 +a^2 )(x^2 +b^2 ))) (1) f(a,b) = (1/(b^2 −a^2 ))∫_0 ^∞ ((1/(x^2 +a^2 ))−(1/(x^2 +b^2 ))) dx f(a,b) = (1/(b^2 −a^2 ))[(1/a)arctan(x/a)−(1/b)arctan(x/b)]_0 ^∞ f(a,b) = (1/(b^2 −a^2 )).(π/2)((1/a)−(1/b)) f(a,b) = (π/(2ab(a+b))) (2) (1) : ((∂f(a,b))/∂a) = −2a∫_0 ^∞ (dx/((x^2 +a^2 )^2 (x^2 +b^2 ))) ((∂^2 f(a,b))/(∂a∂b)) = 4ab∫_0 ^∞ (dx/((x^2 +a^2 )^2 (x^2 +b^2 )^2 )) ((∂^2 f(a,b))/(∂a∂b)) = 4abf(a,b) (3) (2) : ((∂f(a,b))/∂a) = −((π(2a+b))/(2a^2 b(a+b)^2 )) ((∂f^2 (a,b))/(∂a∂b)) = (π/(a^2 b^2 ))[((a^3 +4a^2 b+4ab^2 +b^3 )/((a+b)^4 ))] (4) (3) and (4) : f(a,b) = (π/(4a^3 b^3 ))[((a^3 +4a^2 b+4ab^2 +b^3 )/((a+b)^4 ))] Ω = ∫_0 ^∞ (dx/((x^2 +3)(x^2 +4))) = f((√3),2) ⇒ Ω = (π/( 96(√3)))[((19(√3)+32)/(((√3)+2)^4 ))] Ω = (π/( 96(√3)))(((32+19(√3))/(97+56(√3)))) Ω = (π/( 96(√3)))(51(√3)−88) Ω = (π/4)(((17)/8)−((11(√3))/9))](Q146909.png)
| ||
Question and Answers Forum | ||
Question Number 146835 by mathmax by abdo last updated on 16/Jul/21 | ||
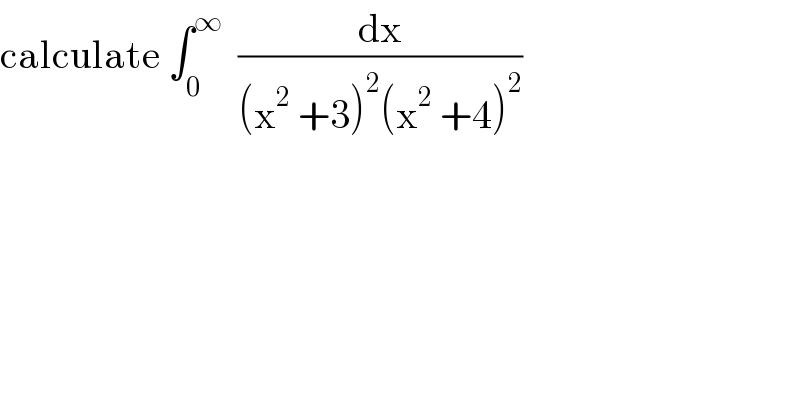 | ||
Answered by mathmax by abdo last updated on 16/Jul/21 | ||
 | ||
| ||
Answered by Olaf_Thorendsen last updated on 16/Jul/21 | ||
![f(a,b) = ∫_0 ^∞ (dx/((x^2 +a^2 )(x^2 +b^2 ))) (1) f(a,b) = (1/(b^2 −a^2 ))∫_0 ^∞ ((1/(x^2 +a^2 ))−(1/(x^2 +b^2 ))) dx f(a,b) = (1/(b^2 −a^2 ))[(1/a)arctan(x/a)−(1/b)arctan(x/b)]_0 ^∞ f(a,b) = (1/(b^2 −a^2 )).(π/2)((1/a)−(1/b)) f(a,b) = (π/(2ab(a+b))) (2) (1) : ((∂f(a,b))/∂a) = −2a∫_0 ^∞ (dx/((x^2 +a^2 )^2 (x^2 +b^2 ))) ((∂^2 f(a,b))/(∂a∂b)) = 4ab∫_0 ^∞ (dx/((x^2 +a^2 )^2 (x^2 +b^2 )^2 )) ((∂^2 f(a,b))/(∂a∂b)) = 4abf(a,b) (3) (2) : ((∂f(a,b))/∂a) = −((π(2a+b))/(2a^2 b(a+b)^2 )) ((∂f^2 (a,b))/(∂a∂b)) = (π/(a^2 b^2 ))[((a^3 +4a^2 b+4ab^2 +b^3 )/((a+b)^4 ))] (4) (3) and (4) : f(a,b) = (π/(4a^3 b^3 ))[((a^3 +4a^2 b+4ab^2 +b^3 )/((a+b)^4 ))] Ω = ∫_0 ^∞ (dx/((x^2 +3)(x^2 +4))) = f((√3),2) ⇒ Ω = (π/( 96(√3)))[((19(√3)+32)/(((√3)+2)^4 ))] Ω = (π/( 96(√3)))(((32+19(√3))/(97+56(√3)))) Ω = (π/( 96(√3)))(51(√3)−88) Ω = (π/4)(((17)/8)−((11(√3))/9))](Q146909.png) | ||
| ||