
Question and Answers Forum
Question Number 146929 by phally last updated on 16/Jul/21
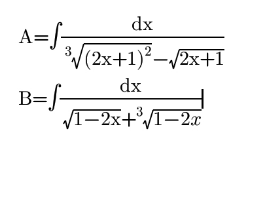
Commented by phally last updated on 16/Jul/21

Commented by tabata last updated on 16/Jul/21
![A)let:y^6 =2x+1⇒3y^5 dy=dx (A)=∫ ((3y^5 )/(y^4 −y^3 ))dy=3∫ ((y^2 −1+1)/(y−1))dy (A)=3∫ [(y+1)+(1/(y−1))]dy=3(y^2 /2)+3y+3 ln∣y−1∣+C replase y by ((2x+1))^(1/6) ∴(A)=∫ (dx/( (((2x+1)^2 ))^(1/3) −(√(2x+1))))=(3/2)((2x+1))^(1/3) +3((2x+1))^(1/6) +3 ln∣((2x+1))^(1/6) −1∣+C ⟨M:T⟩](Q146932.png)
Commented by tabata last updated on 16/Jul/21
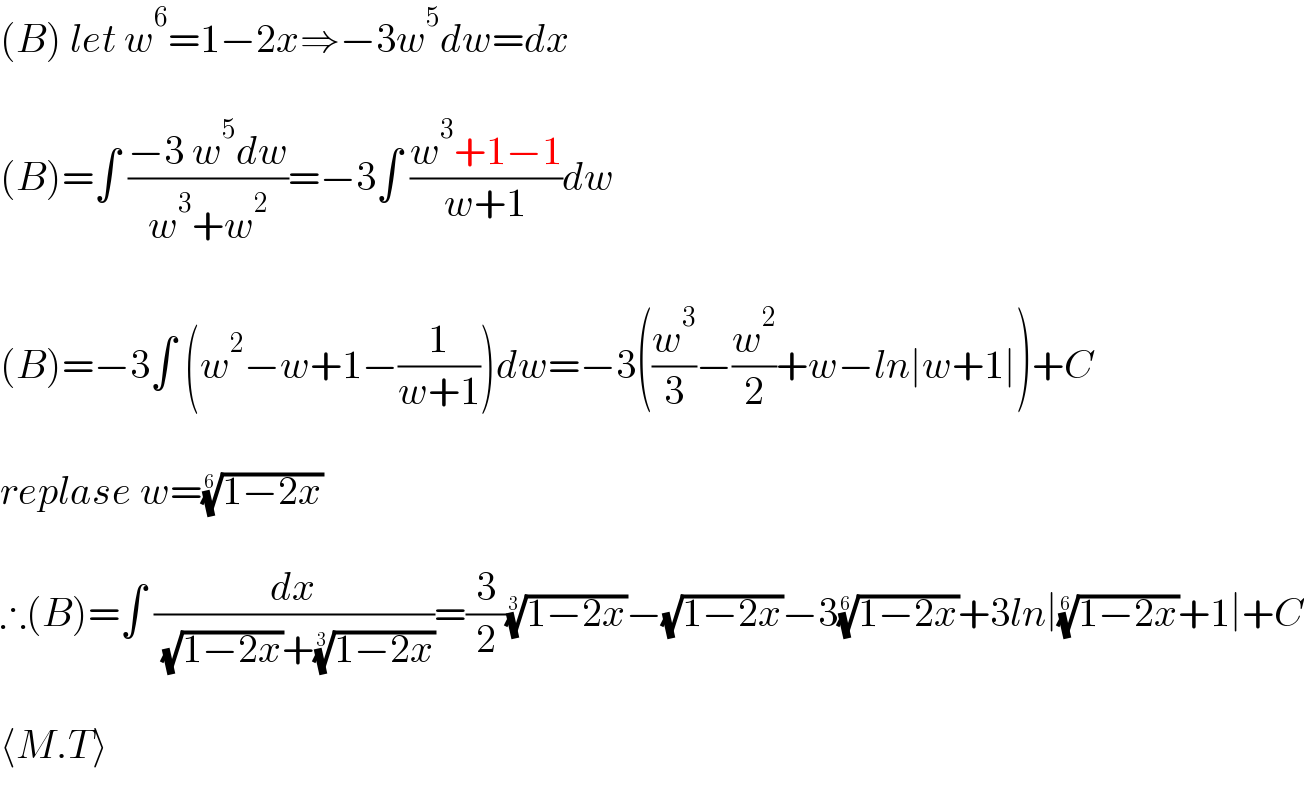
Commented by phally last updated on 16/Jul/21

Commented by tabata last updated on 16/Jul/21

Answered by behi834171 last updated on 16/Jul/21
![A. let: 2x+1=t^6 ⇒t=(2x+1)^(1/6) ,dx=3t^5 dt ⇒A=∫(( 3t^5 dt)/(t^4 −t^3 ))=∫(( 3t^2 dt)/(t−1))=∫(( 3(t^2 −1)+3)/(t−1))dt= =∫3[t+1+(1/(t−1))]dt= =3[(1/2)t^2 +t+ln∣t−1∣+const.= =(3/2)((2x+1))^(1/3) +3((2x+1))^(1/6) +3ln∣[((2x+1))^(1/6) −1]∣+C .■](Q146978.png)
