Question and Answers Forum
Question Number 147195 by mnjuly1970 last updated on 18/Jul/21
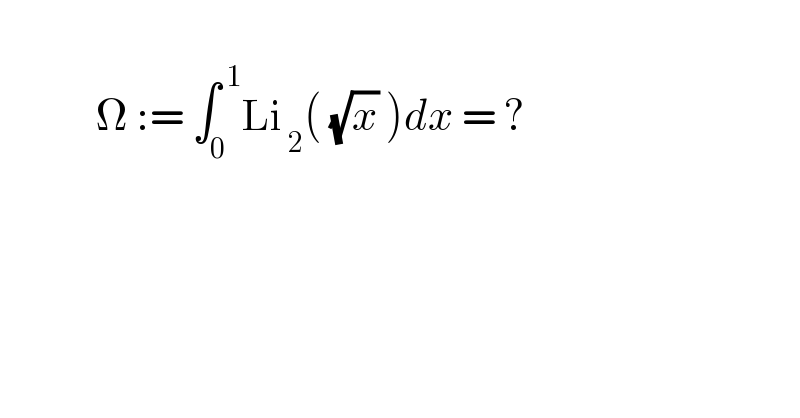
Answered by Olaf_Thorendsen last updated on 18/Jul/21
![Ω = ∫_0 ^1 Li_2 ((√x)) dx Ω = ∫_0 ^1 Σ_(k=1) ^∞ ((((√x))^k )/k^2 ) dx Ω = ∫_0 ^1 Σ_(k=1) ^∞ (x^(k/2) /k^2 ) dx Ω = [Σ_(k=1) ^∞ (x^((k/2)+1) /(k^2 ((k/2)+1)))]_0 ^1 Ω = Σ_(k=1) ^∞ (1/(k^2 ((k/2)+1))) Ω = 2Σ_(k=1) ^∞ (1/(k^2 (k+2))) Ω = Σ_(k=1) ^∞ ((1/k^2 )−(1/2).(1/k)+(1/2).(1/(k+2))) Ω = Σ_(k=1) ^∞ (1/k^2 )−(1/2)Σ_(k=1) ^∞ ((1/k)−(1/(k+2))) Ω = (π^2 /6)−(1/2)(1+(1/2)) Ω = (π^2 /6)−(3/4)](Q147210.png)
Commented by mnjuly1970 last updated on 19/Jul/21
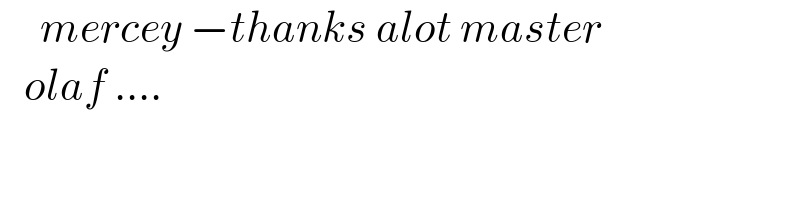
Answered by Kamel last updated on 18/Jul/21
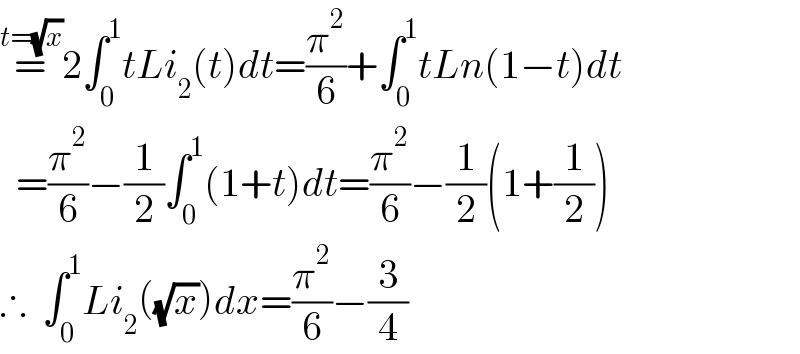
Commented by mnjuly1970 last updated on 19/Jul/21