
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 147205 by mathmax by abdo last updated on 18/Jul/21
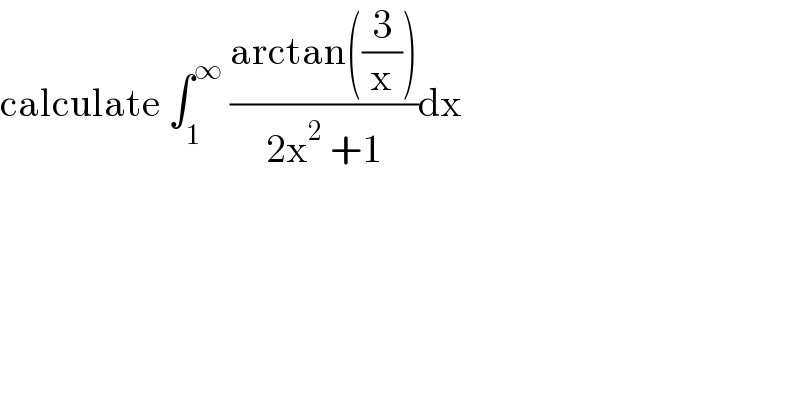
Answered by mathmax by abdo last updated on 20/Jul/21
![Ψ=∫_1 ^∞ ((arctan((3/x)))/(2x^2 +1))dx ⇒Ψ=∫_1 ^∞ (((π/2)−arcan((x/3)))/(2x^2 +1))dx =(π/2)∫_1 ^∞ (dx/(2x^2 +1))−∫_1 ^∞ ((arctan((x/3)))/(2x^2 +1))dx =(π/2)I−J I=(1/2)∫_1 ^∞ (dx/(x^2 +(1/2))) =_(x=(1/( (√2)))y) (1/2)∫_(√2) ^∞ (dy/( (√2)×(1/2)(1+y^2 ))) =(1/( (√2)))[arctany]_(√2) ^∞ =(1/( (√2)))((π/2) −arctan((√2))) we consider f(a)=∫_1 ^∞ ((arctan(ax))/(2x^2 +1))dx (o<a<1) f^′ (a)=∫_1 ^∞ (x/((1+a^2 x^2 )(2x^2 +1)))dx =_(ax=y) ∫_a ^∞ (dy/(a(1+y^2 )(2(y^2 /a^2 ) +1)))=∫_a ^∞ ((a^2 dy)/(a(y^2 +1)(2y^2 +a^2 ))) =a∫_a ^∞ (dy/((y^2 +1)(2y^2 +a^2 )))=2a∫_a ^∞ (dy/((2y^2 +2)(2y^2 +a^2 ))) =((2a)/(a^2 −2)) ∫_a ^∞ ((1/(2y^2 +2))−(1/(2y^2 +a^2 )))dy =(a/(a^2 −2))∫_a ^∞ (dy/(y^2 +1))−(a/(a^2 −2))∫_a ^∞ (dy/(y^2 +(a^2 /2)))(→y=(a/( (√2)))z) =(a/(a^2 −2))((π/2)−arctana)−(a/(a^2 −2)).(a/( (√2)))∫_(√2) ^∞ (dz/((a^2 /2)(1+z^2 ))) =(a/(a^2 −2))((π/2)−arctana)−((√2)/(a^2 −2))((π/2)−arctan((√2))) ⇒ f(a)=∫ {(a/(a^2 −2))((π/2)−arctana)−((√2)/(a^2 −2))((π/2)−arctan(√2))}da ....be continued...](Q147388.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 147205 by mathmax by abdo last updated on 18/Jul/21 | ||
 | ||
Answered by mathmax by abdo last updated on 20/Jul/21 | ||
![Ψ=∫_1 ^∞ ((arctan((3/x)))/(2x^2 +1))dx ⇒Ψ=∫_1 ^∞ (((π/2)−arcan((x/3)))/(2x^2 +1))dx =(π/2)∫_1 ^∞ (dx/(2x^2 +1))−∫_1 ^∞ ((arctan((x/3)))/(2x^2 +1))dx =(π/2)I−J I=(1/2)∫_1 ^∞ (dx/(x^2 +(1/2))) =_(x=(1/( (√2)))y) (1/2)∫_(√2) ^∞ (dy/( (√2)×(1/2)(1+y^2 ))) =(1/( (√2)))[arctany]_(√2) ^∞ =(1/( (√2)))((π/2) −arctan((√2))) we consider f(a)=∫_1 ^∞ ((arctan(ax))/(2x^2 +1))dx (o<a<1) f^′ (a)=∫_1 ^∞ (x/((1+a^2 x^2 )(2x^2 +1)))dx =_(ax=y) ∫_a ^∞ (dy/(a(1+y^2 )(2(y^2 /a^2 ) +1)))=∫_a ^∞ ((a^2 dy)/(a(y^2 +1)(2y^2 +a^2 ))) =a∫_a ^∞ (dy/((y^2 +1)(2y^2 +a^2 )))=2a∫_a ^∞ (dy/((2y^2 +2)(2y^2 +a^2 ))) =((2a)/(a^2 −2)) ∫_a ^∞ ((1/(2y^2 +2))−(1/(2y^2 +a^2 )))dy =(a/(a^2 −2))∫_a ^∞ (dy/(y^2 +1))−(a/(a^2 −2))∫_a ^∞ (dy/(y^2 +(a^2 /2)))(→y=(a/( (√2)))z) =(a/(a^2 −2))((π/2)−arctana)−(a/(a^2 −2)).(a/( (√2)))∫_(√2) ^∞ (dz/((a^2 /2)(1+z^2 ))) =(a/(a^2 −2))((π/2)−arctana)−((√2)/(a^2 −2))((π/2)−arctan((√2))) ⇒ f(a)=∫ {(a/(a^2 −2))((π/2)−arctana)−((√2)/(a^2 −2))((π/2)−arctan(√2))}da ....be continued...](Q147388.png) | ||
| ||