Math Question and Answers


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 147209 by alcohol last updated on 18/Jul/21

Commented by Ar Brandon last updated on 19/Jul/21
$1.∫_(−a) ^a f(x)dx=∫_(−a) ^0 f(x)dx+∫_0 ^a f(x)dx Pour ∫_(−a) ^0 f(x)dx, posons u=−x ⇒du=−dx ⇒∫_(−a) ^0 f(x)dx=−∫_a ^0 f(−u)du=∫_0 ^a f(−u)du=∫_0 ^a f(u)du ⇒∫_(−a) ^a f(x)dx=∫_0 ^a f(x)dx+∫_0 ^a f(x)dx=2∫_0 ^a f(x)dx 2. A_n (F)=(1/π)∫_(−π) ^π F(x)sin(nx)dx F(x) impaire , sin(nx) impaire ⇒F(x)sin(x) paire ⇒A_n (F)=(1/π)∫_(−π) ^π F(x)sin(nx)dx=(2/π)∫_0 ^π F(x)sin(nx)dx ⇒A_n (F)=(2/π)[∫_0 ^(π/2) xsin(nx)dx+∫_(π/2) ^π (π−x)sin(nx)dx] Pour ∫_(π/2) ^π (π−x)sin(nx)dx, u=π−x ⇒du=−dx ⇒∫_(π/2) ^π (π−x)sin(nx)dx=∫_0 ^(π/2) usin(nπ−nu))du = { ((∫_0 ^(π/2) usin(−nu)du si n pair)),((∫_0 ^(π/2) usin(nu)du si n impair)) :}=(−1)^(n+1) ∫_0 ^(π/2) usin(nu)du ⇒A_n (F)=(2/π)[∫_0 ^(π/2) xsin(nx)dx+(−1)^(n+1) ∫_0 ^(π/2) xsin(nx)dx] =(2/π)(1−(−1)^n )∫_0 ^(π/2) xsin(nx)dx 3. A_(2n) (F)=(2/π)(1−(−1)^(2n) )∫_0 ^(π/2) xsin(nx)dx= determinant ((0)), (−1)^(2n) =(1)^n =1 4. A_(2n+1) (F)=(2/π)(1−(−1)^(2n+1) )∫_0 ^(π/2) xsin((2n+1)x)dx =(4/π)∫_0 ^(π/2) xsin((2n+1)x)dx { ((u(x)=x)),((v′(x)=sin((2n+1)x))) :} ⇒ { ((u′(x)=1)),((v(x)=−((cos((2n+1)x))/(2n+1)))) :} A_(2n+1) (F)=(4/π)[−((xcos((2n+1)x))/(2n+1))+(1/(2n+1))∫cos((2n+1)x)dx]_0 ^(π/2) =(4/π)∙(1/((2n+1)))∫_0 ^(π/2) cos((2n+1)x)dx =(4/π)∙(1/((2n+1)^2 ))[sin((2n+1)x)]_0 ^(π/2) =((4(−1)^n )/(π(2n+1)^2 )) 5. F(x)=Σ_(n=0) ^(+∞) A_n (F)sin(nx) =A_0 (F)sin(0)+A_1 (F)sin(x)+A_2 (F)sin(2x)+∙∙∙ A_0 (F)=0, A_2 (F)=0, A_(2n) (F)=0 ⇒F(x)=Σ_(n=0) ^(+∞) A_(2n+1) (F)sin((2n+1)x) =Σ_(n=0) ^(+∞) ((4(−1)^n )/(π(2n+1)^2 ))sin((2n+1)x) Or F(x)= { ((x si 0≤x<(π/2))),((π−x si (π/2)≤x≤π)) :} Prenons F(x)=π−x ⇒π−x=Σ_(n=0) ^(+∞) ((4(−1)^n )/(π(2n+1)^2 ))sin((2n+1)x) Posons x=(π/2) ⇒(π/2)=Σ_(n=0) ^(+∞) ((4(−1)^n )/(π(2n+1)^2 ))sin((2n+1)(π/2))=Σ_(n=0) ^(+∞) ((4(−1)^n ×(−1)^n )/(π(2n+1)^2 )) ⇒Σ_(n=0) ^(+∞) (1/((2n+1)^2 ))=(π^2 /8) b. Σ_(n=1) ^(+∞) (1/n^2 )=1+(1/2^2 )+(1/3^2 )+∙∙∙=(1+(1/3^2 )+∙∙∙)+(1/2^2 )(1+(1/2^2 )+(1/3^2 )+∙∙∙) =Σ_(n=0) ^(+∞) (1/((2n+1)^2 ))+(1/2^2 )Σ_(n=1) ^(+∞) (1/n^2 ) ⇒Σ_(n=1) ^(+∞) (1/n^2 )=(4/3)Σ_(n=0) ^(+∞) (1/((2n+1)^2 ))=(4/3)×(π^2 /8)=(π^2 /6) Σ_(n=1) ^(+∞) (((−1)^(n−1) )/n^2 )=1−(1/2^2 )+(1/3^2 )−(1/4^2 )+∙∙∙ =(1+(1/3^2 )+∙∙∙)−(1/2^2 )(1+(1/2^2 )+∙∙∙)=(π^2 /8)−(1/4)((π^2 /6))=(π^2 /(12))$
$1 . \int_{- a}^{a} f (x) dx = \int_{- a}^{0} f (x) dx + \int_{0}^{a} f (x) dx$ $Pour \int_{- a}^{0} f (x) dx, posons u = - x \Rightarrow du = - dx$ $\Rightarrow \int_{- a}^{0} f (x) dx = - \int_{a}^{0} f (- u) du = \int_{0}^{a} f (- u) du = \int_{0}^{a} f (u) du$ $\Rightarrow \int_{- a}^{a} f (x) dx = \int_{0}^{a} f (x) dx + \int_{0}^{a} f (x) dx = 2 \int_{0}^{a} f (x) dx$ $2 . A_{n} (F) = \frac{1}{π} \int_{- π}^{π} F (x) \sin (nx) dx$ $F (x) impaire, \sin (nx) impaire \Rightarrow F (x) \sin (x) paire$ $\Rightarrow A_{n} (F) = \frac{1}{π} \int_{- π}^{π} F (x) \sin (nx) dx = \frac{2}{π} \int_{0}^{π} F (x) \sin (nx) dx$ $\Rightarrow A_{n} (F) = \frac{2}{π} [\int_{0}^{\frac{π}{2}} xsin (nx) dx + \int_{\frac{π}{2}}^{π} (π - x) \sin (nx) dx]$ $Pour \int_{\frac{π}{2}}^{π} (π - x) \sin (nx) dx, u = π - x \Rightarrow du = - dx$ $\Rightarrow \int_{\frac{π}{2}}^{π} (π - x) \sin (nx) dx = \int_{0}^{\frac{π}{2}} usin (n π - nu)) du$ $= {\begin{cases} \int_{0}^{\frac{π}{2}} usin (- nu) du si n pair \\ \int_{0}^{\frac{π}{2}} usin (nu) du si n impair \end{cases} = {(- 1)}^{n + 1} \int_{0}^{\frac{π}{2}} usin (nu) du$ $\Rightarrow A_{n} (F) = \frac{2}{π} [\int_{0}^{\frac{π}{2}} xsin (nx) dx + {(- 1)}^{n + 1} \int_{0}^{\frac{π}{2}} xsin (nx) dx]$ $= \frac{2}{π} (1 - {(- 1)}^{n}) \int_{0}^{\frac{π}{2}} xsin (nx) dx$ $3 . A_{2 n} (F) = \frac{2}{π} (1 - {(- 1)}^{2 n}) \int_{0}^{\frac{π}{2}} xsin (nx) dx = \begin{matrix} 0 \end{matrix}, {(- 1)}^{2 n} = {(1)}^{n} = 1$ $4 . A_{2 n + 1} (F) = \frac{2}{π} (1 - {(- 1)}^{2 n + 1}) \int_{0}^{\frac{π}{2}} xsin ((2 n + 1) x) dx$ $= \frac{4}{π} \int_{0}^{\frac{π}{2}} xsin ((2 n + 1) x) dx$ ${\begin{cases} u (x) = x \\ v^{'} (x) = \sin ((2 n + 1) x) \end{cases} \Rightarrow {\begin{cases} u^{'} (x) = 1 \\ v (x) = - \frac{\cos ((2 n + 1) x)}{2 n + 1} \end{cases}$ $A_{2 n + 1} (F) = \frac{4}{π} {[- \frac{xcos ((2 n + 1) x)}{2 n + 1} + \frac{1}{2 n + 1} \int \cos ((2 n + 1) x) dx]}_{0}^{\frac{π}{2}}$ $= \frac{4}{π} \cdot \frac{1}{(2 n + 1)} \int_{0}^{\frac{π}{2}} \cos ((2 n + 1) x) dx$ $= \frac{4}{π} \cdot \frac{1}{{(2 n + 1)}^{2}} {[\sin ((2 n + 1) x)]}_{0}^{\frac{π}{2}} = \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}}$ $5 . F (x) = \sum_{n = 0}^{+ \infty} A_{n} (F) \sin (nx)$ $= A_{0} (F) \sin (0) + A_{1} (F) \sin (x) + A_{2} (F) \sin (2 x) + \cdot \cdot \cdot$ $A_{0} (F) = 0, A_{2} (F) = 0, A_{2 n} (F) = 0$ $\Rightarrow F (x) = \sum_{n = 0}^{+ \infty} A_{2 n + 1} (F) \sin ((2 n + 1) x)$ $= \sum_{n = 0}^{+ \infty} \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} \sin ((2 n + 1) x)$ $Or F (x) = {\begin{cases} x si 0 ⩽ x < \frac{π}{2} \\ π - x si \frac{π}{2} ⩽ x ⩽ π \end{cases}$ $Prenons F (x) = π - x$ $\Rightarrow π - x = \sum_{n = 0}^{+ \infty} \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} \sin ((2 n + 1) x)$ $Posons x = \frac{π}{2}$ $\Rightarrow \frac{π}{2} = \sum_{n = 0}^{+ \infty} \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} \sin ((2 n + 1) \frac{π}{2}) = \sum_{n = 0}^{+ \infty} \frac{4 {(- 1)}^{n} \times {(- 1)}^{n}}{π {(2 n + 1)}^{2}}$ $\Rightarrow \sum_{n = 0}^{+ \infty} \frac{1}{{(2 n + 1)}^{2}} = \frac{π^{2}}{8}$ $b . \sum_{n = 1}^{+ \infty} \frac{1}{n^{2}} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdot \cdot \cdot = (1 + \frac{1}{3^{2}} + \cdot \cdot \cdot) + \frac{1}{2^{2}} (1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdot \cdot \cdot)$ $= \sum_{n = 0}^{+ \infty} \frac{1}{{(2 n + 1)}^{2}} + \frac{1}{2^{2}} \sum_{n = 1}^{+ \infty} \frac{1}{n^{2}}$ $\Rightarrow \sum_{n = 1}^{+ \infty} \frac{1}{n^{2}} = \frac{4}{3} \sum_{n = 0}^{+ \infty} \frac{1}{{(2 n + 1)}^{2}} = \frac{4}{3} \times \frac{π^{2}}{8} = \frac{π^{2}}{6}$ $\sum_{n = 1}^{+ \infty} \frac{{(- 1)}^{n - 1}}{n^{2}} = 1 - \frac{1}{2^{2}} + \frac{1}{3^{2}} - \frac{1}{4^{2}} + \cdot \cdot \cdot$ $= (1 + \frac{1}{3^{2}} + \cdot \cdot \cdot) - \frac{1}{2^{2}} (1 + \frac{1}{2^{2}} + \cdot \cdot \cdot) = \frac{π^{2}}{8} - \frac{1}{4} (\frac{π^{2}}{6}) = \frac{π^{2}}{12}$
	Answered by puissant last updated on 19/Jul/21

	$5)$ $a)$ $F (x) = \underset{n = 0}{\sum^{\infty}} A_{n} (F) \sin (nx)$ $F (x) = \underset{n = 0}{\sum^{\infty}} A_{2 n + 1} (F) \sin ((2 n + 1) x)$ $\Rightarrow F (x) = \underset{n = 0}{\sum^{\infty}} \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} \sin ((2 n + 1) x)$ $posons F (x) = π - x$ $\Rightarrow π - x = \underset{n = 0}{\sum^{\infty}} \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} \sin ((2 n + 1) x)$ $posons x = \frac{π}{2} . .$ $\Rightarrow \frac{π}{2} = \underset{n = 0}{\sum^{\infty}} \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} \sin ((2 n + 1) \frac{π}{2})$ $\sin ((2 n + 1) \frac{π}{2}) = {(- 1)}^{n}; \forall n \in N$ $\Rightarrow \frac{π}{2} = \frac{4}{π} \underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{2 n}}{{(2 n + 1)}^{2}}$ $soit \underset{n = 0}{\sum^{\infty}} \frac{1}{{(2 n + 1)}^{2}} = \frac{π^{2}}{8} . . .$ $b)$ $\underset{n = 1}{\sum^{\infty}} \frac{1}{n^{2}} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \frac{1}{5^{2}} + . . . . . . . .$ $= (1 + \frac{1}{3^{2}} + \frac{1}{5^{2}} + . . . .) + \frac{1}{2^{2}} (1 + \frac{1}{2^{2}} + \frac{1}{4^{2}} + . . . . .)$ $\Rightarrow \underset{n = 0}{\sum^{\infty}} \frac{1}{n^{2}} = \underset{n = 0}{\sum^{\infty}} \frac{1}{{(2 n + 1)}^{2}} + \frac{1}{4} \underset{n = 0}{\sum^{\infty}} \frac{1}{n^{2}}$ $\Rightarrow \frac{3}{4} \underset{n = 0}{\sum^{\infty}} \frac{1}{n^{2}} = \underset{n = 0}{\sum^{\infty}} \frac{1}{{(2 n + 1)}^{2}} = \frac{π^{2}}{8}$ $\Rightarrow \underset{n = 0}{\sum^{\infty}} \frac{1}{n^{2}} = \frac{4}{3} \times \frac{π^{2}}{8}$ $soit \underset{n = 0}{\sum^{\infty}} \frac{1}{n^{2}} = \frac{π^{2}}{6} . . .$ $c)$ $\underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n^{2}} = 1 - \frac{1}{2^{2}} + \frac{1}{3^{2}} - \frac{1}{4^{2}} + . . . . . .$ $= (1 + \frac{1}{3^{2}} + \frac{1}{5^{2}} + . . . .) - \frac{1}{2^{2}} (1 + \frac{1}{2^{2}} + \frac{1}{4^{2}} + . . . .)$ $= \frac{π^{2}}{8} - \frac{1}{4} \times \frac{π^{2}}{6} = \frac{π^{2}}{8} - \frac{π^{2}}{24} = \frac{π^{2}}{12} . .$ $soit \underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n^{2}} = \frac{π^{2}}{12} . . . .$
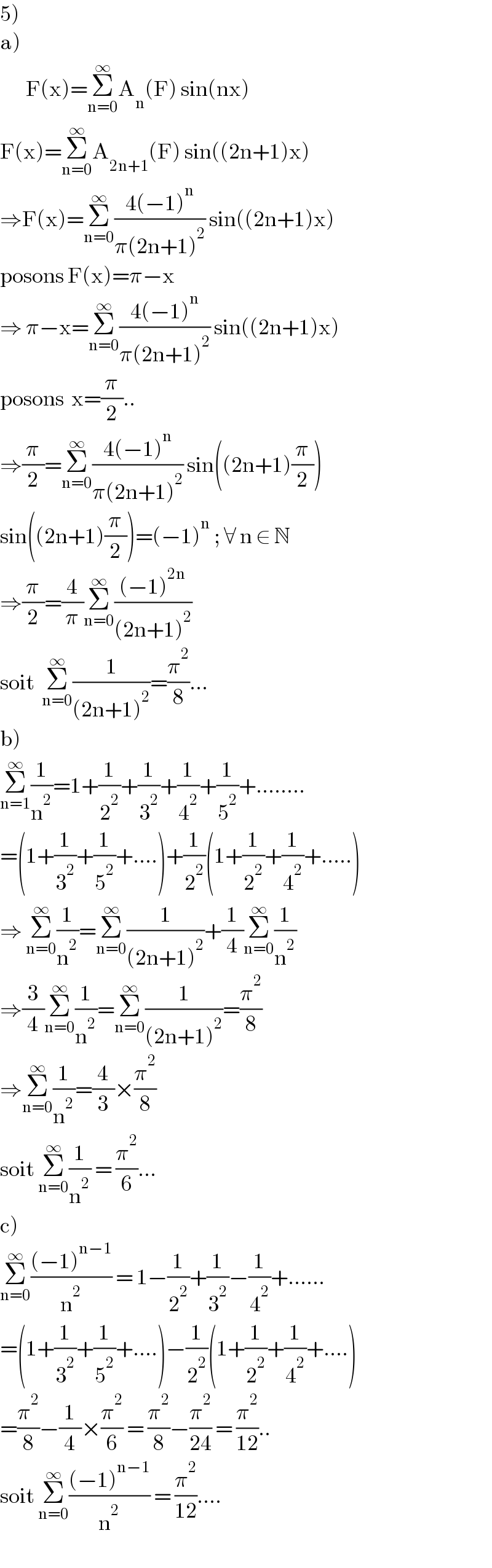
	Commented by alcohol last updated on 19/Jul/21

	$m e r c i$ $l a 1, 2, 3, 4 p a r d o n$
	Answered by puissant last updated on 19/Jul/21
	$1) ∫_(−a) ^a f(x)dx=∫_(−a) ^0 f(x)dx+∫_0 ^( a) f(x)dx pour ∫_(−a) ^( 0) f(x)dx , posons t=−x ⇒ dt=−dx ⇒∫_(−a) ^( 0) f(x)dx=∫_0 ^( a) f(−t)dt=∫_0 ^( a) f(x)dx car la fonction est paire et les vaiables sont muettes.. ⇒∫_(−a) ^( a) f(x)dx=∫_0 ^( a) f(x)dx+∫_0 ^( a) f(x)dx=2∫_0 ^( a) f(x)dx.. 2) A_n (F)=(1/π)∫_(−π) ^( π) F(x)sin(nx)dx F(x) est impair et sin(nx) est impair donc F(x)sin(nx) est paire, ainsi on a: A_n (F)=(2/π)∫_0 ^( π) F(x)sin(nx)dx ⇒ A_n (F)=(2/π)∫_0 ^( (π/2)) xsin(nx)dx+(2/π)∫_(π/2) ^( π) (π−x)sin(nx)dx disons Q=∫_(π/2) ^( π) (π−x)sin(nx)dx posons u=π−x ⇒ du=−dx Q=−∫_(π/2) ^( 0) usin(nπ−nu)du=∫_0 ^( (π/2)) usin(nπ−nu)du →si n paire, Q=∫_0 ^(π/2) usin(−nu)du → si n impaire, Q=∫_0 ^(π/2) usin(nu)du d′ou Q=(−1)^(n+1) ∫_0 ^(π/2) usin(nu)du A_n (F)=(2/π)(∫_0 ^(π/2) xsin(nx)dx+(−1)^(n+1) ∫_0 ^(π/2) xsin(nx)dx) soit A_n (F)=(2/π)(1−(−1)^n )∫_0 ^(π/2) xsin(nx)dx... 3) A_(2n) (F)=(2/π)(1−(−1)^(2n) )∫_0 ^(π/2) xsin(nx)dx=0 car 1−(−1)^(2n) =1−1=0.. 4) A_(2n+1) (F)=(2/π)(1−(−1)^(2n+1) )∫_0 ^(π/2) xsin((2n+1)x)dx =(4/π)∫_0 ^(π/2) xsin((2n+1)x)dx alors, posons { ((u=x)),((v′=sin((2n+1)x))) :}⇒ { ((u′=1)),((v=−(1/(2n+1))cos((2n+1)x))) :} A_(2n+1) (F)=(4/π)[−(x/(2n+1))cos((2n+1)x)]_0 ^(π/2) +(4/(π(2n+1)))∫_0 ^( (π/2)) cos((2n+1)x)dx =(4/(π(2n+1)))∫_0 ^( (π/2)) cos((2n+1)x)dx =(4/(π(2n+1)^2 ))[sin((2n+1)x)]_0 ^(π/2) =((4(−1)^n )/(π(2n+1)^2 )).. car sin((2n+1)(π/2))=(−1)^n$
	$1)$ $\int_{- a}^{a} f (x) dx = \int_{- a}^{0} f (x) dx + \int_{0}^{a} f (x) dx$ $pour \int_{- a}^{0} f (x) dx, posons t = - x \Rightarrow dt = - dx$ $\Rightarrow \int_{- a}^{0} f (x) dx = \int_{0}^{a} f (- t) dt = \int_{0}^{a} f (x) dx$ $car la fonction est paire et les vaiables sont muettes . .$ $\Rightarrow \int_{- a}^{a} f (x) dx = \int_{0}^{a} f (x) dx + \int_{0}^{a} f (x) dx = 2 \int_{0}^{a} f (x) dx . .$ $2)$ $A_{n} (F) = \frac{1}{π} \int_{- π}^{π} F (x) \sin (nx) dx$ $F (x) est impair et \sin (nx) est impair donc$ $F (x) \sin (nx) est paire, ainsi on a :$ $A_{n} (F) = \frac{2}{π} \int_{0}^{π} F (x) \sin (nx) dx$ $\Rightarrow A_{n} (F) = \frac{2}{π} \int_{0}^{\frac{π}{2}} xsin (nx) dx + \frac{2}{π} \int_{\frac{π}{2}}^{π} (π - x) \sin (nx) dx$ $disons Q = \int_{\frac{π}{2}}^{π} (π - x) \sin (nx) dx$ $posons u = π - x \Rightarrow du = - dx$ $Q = - \int_{\frac{π}{2}}^{0} usin (n π - nu) du = \int_{0}^{\frac{π}{2}} usin (n π - nu) du$ $\to si n paire, Q = \int_{0}^{\frac{π}{2}} usin (- nu) du$ $\to si n impaire, Q = \int_{0}^{\frac{π}{2}} usin (nu) du$ $d^{'} ou Q = {(- 1)}^{n + 1} \int_{0}^{\frac{π}{2}} usin (nu) du$ $A_{n} (F) = \frac{2}{π} (\int_{0}^{\frac{π}{2}} xsin (nx) dx + {(- 1)}^{n + 1} \int_{0}^{\frac{π}{2}} xsin (nx) dx)$ $soit A_{n} (F) = \frac{2}{π} (1 - {(- 1)}^{n}) \int_{0}^{\frac{π}{2}} xsin (nx) dx . . .$ $3)$ $A_{2 n} (F) = \frac{2}{π} (1 - {(- 1)}^{2 n}) \int_{0}^{\frac{π}{2}} xsin (nx) dx = 0$ $car 1 - {(- 1)}^{2 n} = 1 - 1 = 0 . .$ $4)$ $A_{2 n + 1} (F) = \frac{2}{π} (1 - {(- 1)}^{2 n + 1}) \int_{0}^{\frac{π}{2}} xsin ((2 n + 1) x) dx$ $= \frac{4}{π} \int_{0}^{\frac{π}{2}} xsin ((2 n + 1) x) dx$ $alors, posons {\begin{cases} u = x \\ v^{'} = \sin ((2 n + 1) x) \end{cases} \Rightarrow {\begin{cases} u^{'} = 1 \\ v = - \frac{1}{2 n + 1} \cos ((2 n + 1) x) \end{cases}$ $A_{2 n + 1} (F) = \frac{4}{π} {[- \frac{x}{2 n + 1} \cos ((2 n + 1) x)]}_{0}^{\frac{π}{2}} + \frac{4}{π (2 n + 1)} \int_{0}^{\frac{π}{2}} \cos ((2 n + 1) x) dx$ $= \frac{4}{π (2 n + 1)} \int_{0}^{\frac{π}{2}} \cos ((2 n + 1) x) dx$ $= \frac{4}{π {(2 n + 1)}^{2}} {[\sin ((2 n + 1) x)]}_{0}^{\frac{π}{2}}$ $= \frac{4 {(- 1)}^{n}}{π {(2 n + 1)}^{2}} . . car \sin ((2 n + 1) \frac{π}{2}) = {(- 1)}^{n}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum