Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 147309 by puissant last updated on 19/Jul/21

Answered by mathmax by abdo last updated on 19/Jul/21

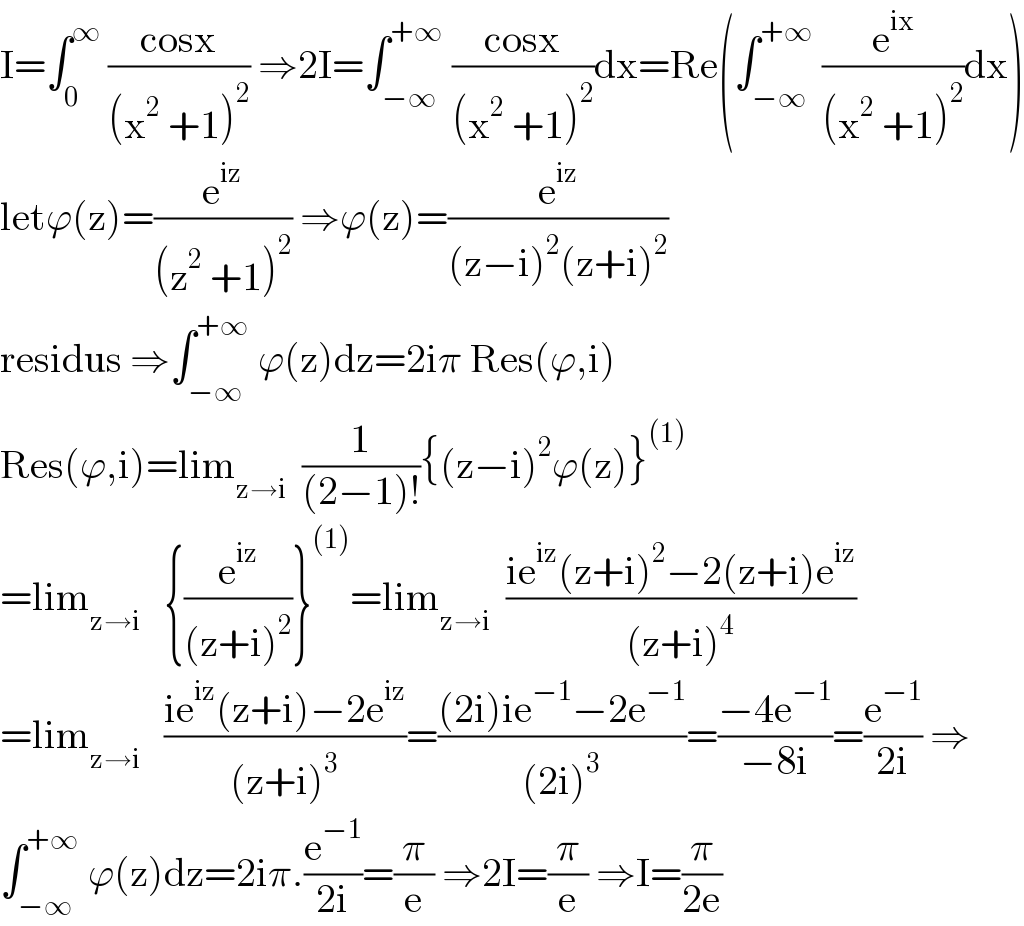
I=∫_0 ^∞ ((cosx)/((x^2 +1)^2 )) ⇒2I=∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^2 ))dx=Re(∫_(−∞) ^(+∞) (e^(ix) /((x^2 +1)^2 ))dx) letϕ(z)=(e^(iz) /((z^2 +1)^2 )) ⇒ϕ(z)=(e^(iz) /((z−i)^2 (z+i)^2 )) residus ⇒∫_(−∞) ^(+∞) ϕ(z)dz=2iπ Res(ϕ,i) Res(ϕ,i)=lim_(z→i) (1/((2−1)!)){(z−i)^2 ϕ(z)}^((1)) =lim_(z→i) {(e^(iz) /((z+i)^2 ))}^((1)) =lim_(z→i) ((ie^(iz) (z+i)^2 −2(z+i)e^(iz) )/((z+i)^4 )) =lim_(z→i) ((ie^(iz) (z+i)−2e^(iz) )/((z+i)^3 ))=(((2i)ie^(−1) −2e^(−1) )/((2i)^3 ))=((−4e^(−1) )/(−8i))=(e^(−1) /(2i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ.(e^(−1) /(2i))=(π/e) ⇒2I=(π/e) ⇒I=(π/(2e))

$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{2I}=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{ix}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right) \\ $$$$\mathrm{let}\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\mathrm{residus}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:\:\: \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} =\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{ie}^{\mathrm{iz}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{ie}^{\mathrm{iz}} \left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2e}^{\mathrm{iz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} }=\frac{\left(\mathrm{2i}\right)\mathrm{ie}^{−\mathrm{1}} −\mathrm{2e}^{−\mathrm{1}} }{\left(\mathrm{2i}\right)^{\mathrm{3}} }=\frac{−\mathrm{4e}^{−\mathrm{1}} }{−\mathrm{8i}}=\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{2i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi.\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{2i}}=\frac{\pi}{\mathrm{e}}\:\Rightarrow\mathrm{2I}=\frac{\pi}{\mathrm{e}}\:\Rightarrow\mathrm{I}=\frac{\pi}{\mathrm{2e}} \\ $$

Commented by puissant last updated on 19/Jul/21

thanks

$${thanks} \\ $$

Answered by mathmax by abdo last updated on 19/Jul/21

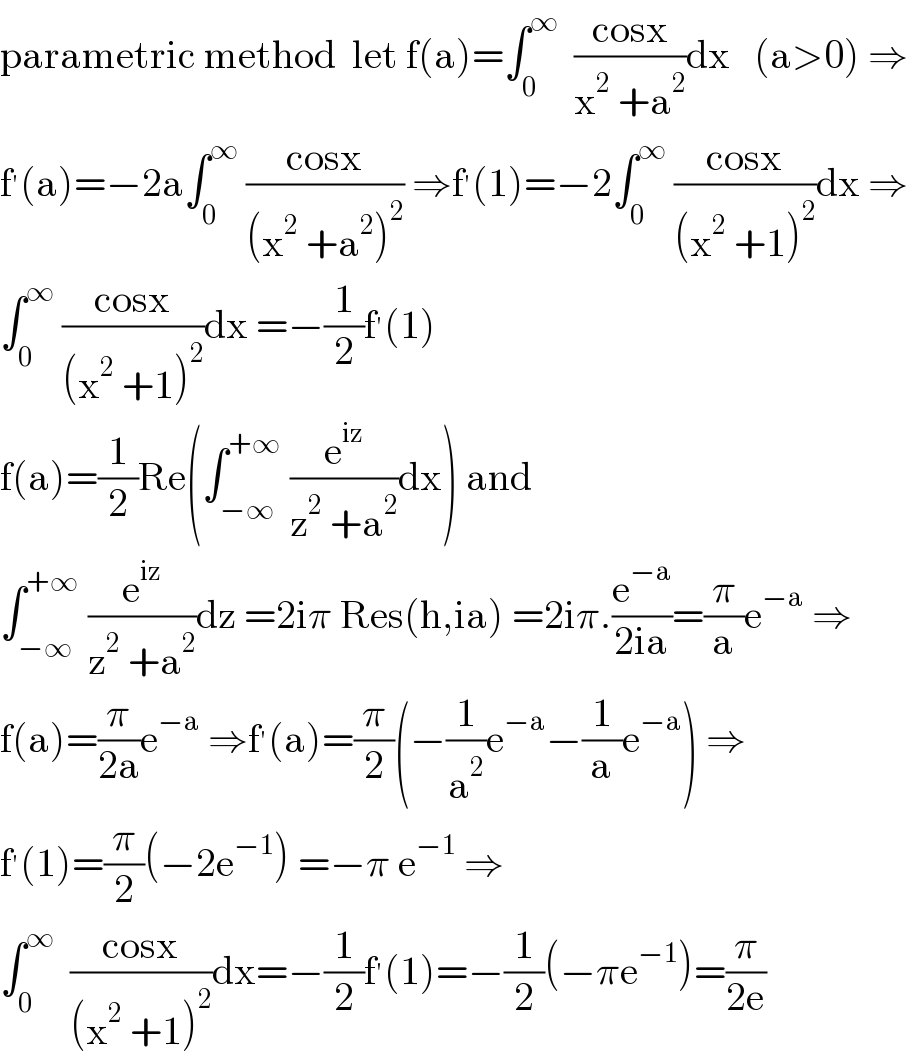
parametric method let f(a)=∫_0 ^∞ ((cosx)/(x^2 +a^2 ))dx (a>0) ⇒ f^′ (a)=−2a∫_0 ^∞ ((cosx)/((x^2 +a^2 )^2 )) ⇒f^′ (1)=−2∫_0 ^∞ ((cosx)/((x^2 +1)^2 ))dx ⇒ ∫_0 ^∞ ((cosx)/((x^2 +1)^2 ))dx =−(1/2)f^′ (1) f(a)=(1/2)Re(∫_(−∞) ^(+∞) (e^(iz) /(z^2 +a^2 ))dx) and ∫_(−∞) ^(+∞) (e^(iz) /(z^2 +a^2 ))dz =2iπ Res(h,ia) =2iπ.(e^(−a) /(2ia))=(π/a)e^(−a) ⇒ f(a)=(π/(2a))e^(−a) ⇒f^′ (a)=(π/2)(−(1/a^2 )e^(−a) −(1/a)e^(−a) ) ⇒ f^′ (1)=(π/2)(−2e^(−1) ) =−π e^(−1) ⇒ ∫_0 ^∞ ((cosx)/((x^2 +1)^2 ))dx=−(1/2)f^′ (1)=−(1/2)(−πe^(−1) )=(π/(2e))

$$\mathrm{parametric}\:\mathrm{method}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\:\:\left(\mathrm{a}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\mathrm{2a}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}^{'} \left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{iz}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{iz}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{h},\mathrm{ia}\right)\:=\mathrm{2i}\pi.\frac{\mathrm{e}^{−\mathrm{a}} }{\mathrm{2ia}}=\frac{\pi}{\mathrm{a}}\mathrm{e}^{−\mathrm{a}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{2a}}\mathrm{e}^{−\mathrm{a}} \:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\pi}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{e}^{−\mathrm{a}} −\frac{\mathrm{1}}{\mathrm{a}}\mathrm{e}^{−\mathrm{a}} \right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}\left(−\mathrm{2e}^{−\mathrm{1}} \right)\:=−\pi\:\mathrm{e}^{−\mathrm{1}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}^{'} \left(\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\left(−\pi\mathrm{e}^{−\mathrm{1}} \right)=\frac{\pi}{\mathrm{2e}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com