
Question and Answers Forum
Question Number 147364 by henderson last updated on 20/Jul/21
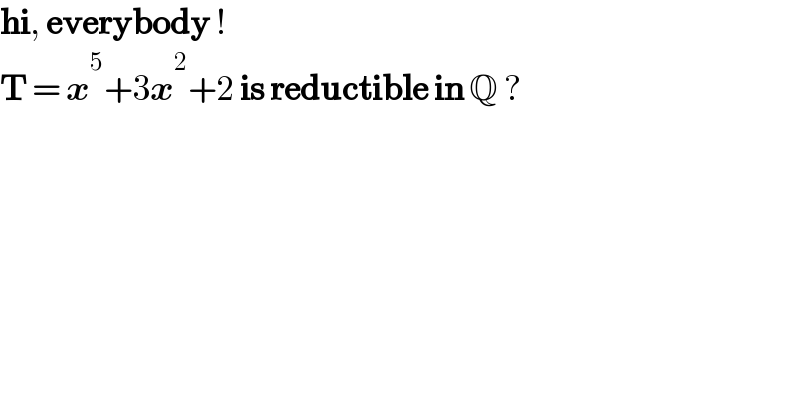
Answered by Olaf_Thorendsen last updated on 20/Jul/21
![T∈Q[X], T(x) = x^5 +3x^2 +2 T(x) = x^5 +3x^2 +2 It′s easy to verify with the sign of T′(x) that T has only one real root. Then T is not reductible in Q, in R. Only in C.](Q147386.png)
Answered by puissant last updated on 20/Jul/21
![P is a polynomial.. P(X)=a_n X^n +a_(n−1) X^(n−1) +....+a_1 X+a_0 ∃ p ( prime number)/ • p split a_0 , a_1 , ..... , a_(n−1) • p no split a_n • p^2 no split a_0 ⇒ P is irreductible in Q[x] (Einsentein theorem)...](Q147389.png)
Commented by Olaf_Thorendsen last updated on 20/Jul/21

Commented by puissant last updated on 20/Jul/21
Commented by Olaf_Thorendsen last updated on 20/Jul/21

Commented by puissant last updated on 20/Jul/21

