Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 147371 by mathdanisur last updated on 20/Jul/21

$$ifx>0then:$$ $$e^{\mathit{x}+{\mathit{e}}^{-\mathit{x}}}+e^{-\mathit{x}+{\mathit{e}}^{\mathit{x}}}⩾2coshx\cdot e^{\mathit{s}\mathit{e}\mathit{c}\mathit{h}\mathit{x}}$$

Answered by mindispower last updated on 20/Jul/21

$$a+b⩾2\sqrt{ab}$$ $$\Rightarrow a=e^{x+e^{-x}},b=e^{-x+e^x}$$ $$⩾2\sqrt{e^{x+e^{-x}-x+e^x}}=2e^{ch\left(x\right)}$$ $$2e^{ch\left(x\right)}⩾2ch\left(x\right)e^{\frac{1}{ch\left(x\right)}}......(?)$$ $$t=ch\left(x\right)⩾ch\left(0\right)=1$$ $$2e^x⩾2{xe}^{\frac{1}{x}}....\mathrm{\forall }x⩾1\iff$$ $$e^{x-\frac{1}{x}}⩾x,x⩾1$$ $$f\left(x\right)=e^{x-\frac{1}{x}}-x$$ $$f^{\prime }\left(x\right)=(1+\frac{1}{x^2})e^{x-\frac{1}{x}}-1⩾$$ $$x⩾1\Rightarrow x-\frac{1}{x}⩾1-1=0$$ $$\Rightarrow f^{\prime }\left(x\right)⩾1+\frac{1}{x^2}-1>0$$ $$fisincreasing$$ $$f\left(x\right)⩾f\left(1\right)=e^0-1=0$$ $$\Rightarrow f\left(x\right)⩾0then$$ $$justdeduce$$ $$$$ $$$$

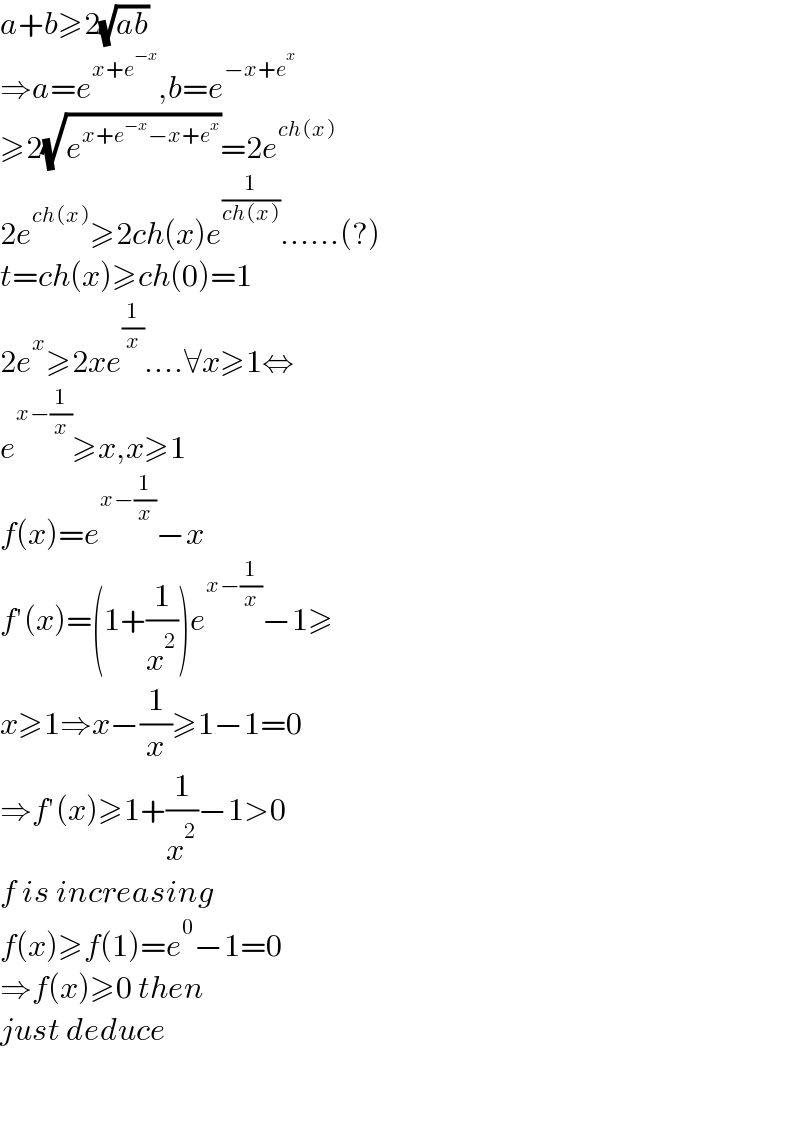
Commented bymathdanisur last updated on 23/Jul/21

$$pleaseSir$$

Commented bymathdanisur last updated on 20/Jul/21

$$thankyouSer,please{it}^{\prime }sextent$$

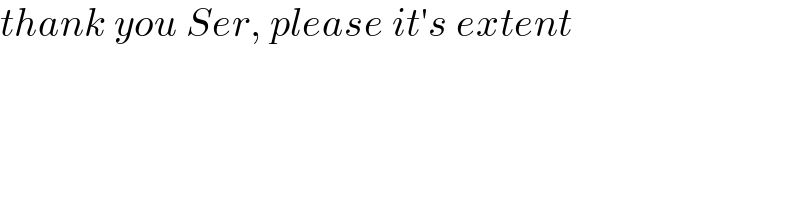
Commented bymindispower last updated on 21/Jul/21

$$justreplacex=ch\left(t\right)$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com