Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 147467 by mathmax by abdo last updated on 21/Jul/21

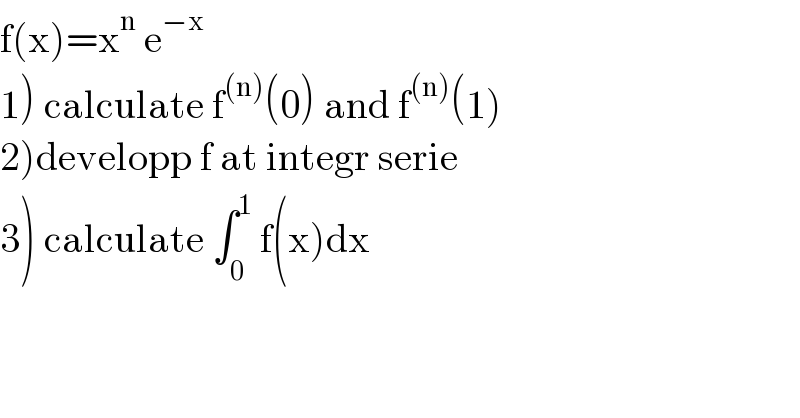
f(x)=x^n e^(−x) 1) calculate f^((n)) (0) and f^((n)) (1) 2)developp f at integr serie 3) calculate ∫_0 ^1 f(x)dx

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{x}} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Answered by mathmax by abdo last updated on 22/Jul/21

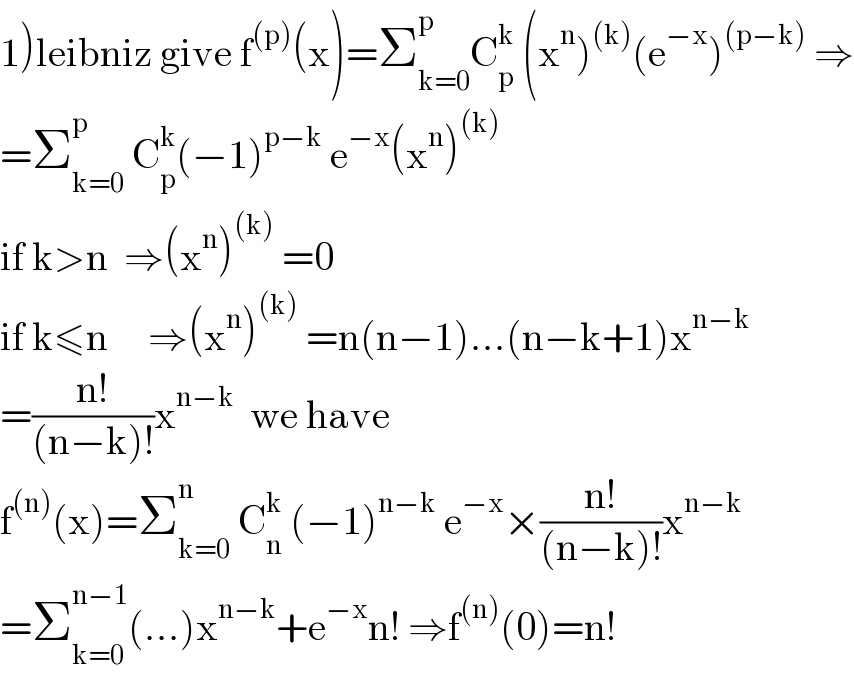
1)leibniz give f^((p)) (x)=Σ_(k=0) ^p C_p ^k (x^n )^((k)) (e^(−x) )^((p−k)) ⇒ =Σ_(k=0) ^p C_p ^k (−1)^(p−k) e^(−x) (x^n )^((k)) if k>n ⇒(x^n )^((k)) =0 if k≤n ⇒(x^n )^((k)) =n(n−1)...(n−k+1)x^(n−k) =((n!)/((n−k)!))x^(n−k) we have f^((n)) (x)=Σ_(k=0) ^n C_n ^k (−1)^(n−k) e^(−x) ×((n!)/((n−k)!))x^(n−k) =Σ_(k=0) ^(n−1) (...)x^(n−k) +e^(−x) n! ⇒f^((n)) (0)=n!

$$\left.\mathrm{1}\right)\mathrm{leibniz}\:\mathrm{give}\:\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{p}} \mathrm{C}_{\mathrm{p}} ^{\mathrm{k}} \:\left(\mathrm{x}^{\mathrm{n}} \right)^{\left(\mathrm{k}\right)} \left(\mathrm{e}^{−\mathrm{x}} \right)^{\left(\mathrm{p}−\mathrm{k}\right)} \:\Rightarrow \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{p}} \:\mathrm{C}_{\mathrm{p}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{x}} \left(\mathrm{x}^{\mathrm{n}} \right)^{\left(\mathrm{k}\right)} \\ $$$$\mathrm{if}\:\mathrm{k}>\mathrm{n}\:\:\Rightarrow\left(\mathrm{x}^{\mathrm{n}} \right)^{\left(\mathrm{k}\right)} \:=\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{k}\leqslant\mathrm{n}\:\:\:\:\:\Rightarrow\left(\mathrm{x}^{\mathrm{n}} \right)^{\left(\mathrm{k}\right)} \:=\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)...\left(\mathrm{n}−\mathrm{k}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{k}} \\ $$$$=\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{k}\right)!}\mathrm{x}^{\mathrm{n}−\mathrm{k}} \:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{x}} ×\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{k}\right)!}\mathrm{x}^{\mathrm{n}−\mathrm{k}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(...\right)\mathrm{x}^{\mathrm{n}−\mathrm{k}} +\mathrm{e}^{−\mathrm{x}} \mathrm{n}!\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)=\mathrm{n}! \\ $$

Commented by mathmax by abdo last updated on 22/Jul/21

f^((n)) (1)=e^(−1) Σ_(k=0) ^n (−1)^(n−k) ((n!)/(k!(n−k)!))×((n!)/((n−k)!)) =(−1)^n e^(−1) Σ_(k=0) ^n (((−1)^k )/(k!))×(((n!)^2 )/(((n−k)!)^2 ))

$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right)=\mathrm{e}^{−\mathrm{1}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{k}} \:\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!}×\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{k}\right)!} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{e}^{−\mathrm{1}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!}×\frac{\left(\mathrm{n}!\right)^{\mathrm{2}} }{\left(\left(\mathrm{n}−\mathrm{k}\right)!\right)^{\mathrm{2}} } \\ $$

Answered by mathmax by abdo last updated on 22/Jul/21

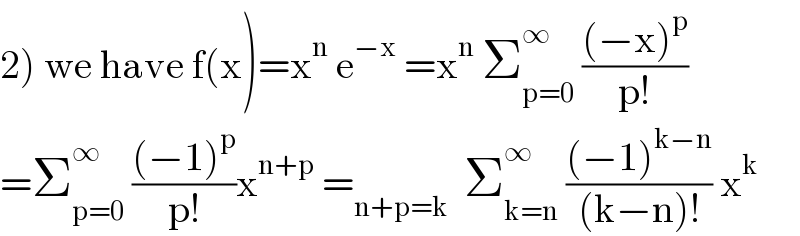
2) we have f(x)=x^n e^(−x) =x^n Σ_(p=0) ^∞ (((−x)^p )/(p!)) =Σ_(p=0) ^∞ (((−1)^p )/(p!))x^(n+p) =_(n+p=k) Σ_(k=n) ^∞ (((−1)^(k−n) )/((k−n)!)) x^k

$$\left.\mathrm{2}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{x}} \:=\mathrm{x}^{\mathrm{n}} \:\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{x}\right)^{\mathrm{p}} }{\mathrm{p}!} \\ $$$$=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\mathrm{p}!}\mathrm{x}^{\mathrm{n}+\mathrm{p}} \:=_{\mathrm{n}+\mathrm{p}=\mathrm{k}} \:\:\sum_{\mathrm{k}=\mathrm{n}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{n}} }{\left(\mathrm{k}−\mathrm{n}\right)!}\:\mathrm{x}^{\mathrm{k}} \\ $$

Answered by mathmax by abdo last updated on 22/Jul/21

3) A_n =∫_0 ^1 x^n e^(−x) dx by parts we get A_n =[(x^(n+1) /(n+1))e^(−x) ]_0 ^1 +∫_0 ^1 (x^(n+1) /(n+1))e^(−x) dx=(e^(−1) /(n+1)) +(1/(n+1)) A_(n+1) ⇒ (n+1)A_n =(1/e) +A_(n+1) ⇒A_(n+1) =(n+1)A_n −(1/e) ⇒ A_n =nA_(n−1) −(1/e) let u_n =(A_n /(n!)) ⇒ u_(n+1) =(A_(n+1) /((n+1)!))=(((n+1)A_n −(1/e))/((n+1)!))=(A_n /(n!))−(1/(e(n+1)!)) =u_n −(1/(e(n+1)!)) ⇒u_(n+1) −u_n =−(1/(e(n+1)!)) ⇒ Σ_(k=0) ^n (u_(k+1) −u_k )=−(1/e)Σ_(k=0) ^n (1/((k+1)!)) ⇒ u_n −u_0 =−(1/e)Σ_(k=1) ^(n+1) (1/(k!)) ⇒u_n =u_o −(1/e)Σ_(k=1) ^(n+1) (1/(k!)) u_o =A_0 =∫_0 ^1 e^(−x) dx=[−e^(−x) ]_0 ^1 =1−(1/e) ⇒ u_n =1−(1/e)Σ_(k=0) ^(n+1 ) (1/(k!)) A_n =n!u_n =n!(1−(1/e)Σ_(k=0) ^(n+1) (1/(k!)))

$$\left.\mathrm{3}\right)\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\:\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{A}_{\mathrm{n}} =\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{e}^{−\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}=\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\mathrm{A}_{\mathrm{n}+\mathrm{1}} \:\Rightarrow \\ $$$$\left(\mathrm{n}+\mathrm{1}\right)\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{e}}\:+\mathrm{A}_{\mathrm{n}+\mathrm{1}} \:\Rightarrow\mathrm{A}_{\mathrm{n}+\mathrm{1}} =\left(\mathrm{n}+\mathrm{1}\right)\mathrm{A}_{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{e}}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{nA}_{\mathrm{n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{e}}\:\:\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{A}_{\mathrm{n}} }{\mathrm{n}!}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{A}_{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)!}=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{A}_{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{e}}}{\left(\mathrm{n}+\mathrm{1}\right)!}=\frac{\mathrm{A}_{\mathrm{n}} }{\mathrm{n}!}−\frac{\mathrm{1}}{\mathrm{e}\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$$$=\mathrm{u}_{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{e}\left(\mathrm{n}+\mathrm{1}\right)!}\:\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{u}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{e}\left(\mathrm{n}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{u}_{\mathrm{k}+\mathrm{1}} −\mathrm{u}_{\mathrm{k}} \right)=−\frac{\mathrm{1}}{\mathrm{e}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} −\mathrm{u}_{\mathrm{0}} =−\frac{\mathrm{1}}{\mathrm{e}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}!}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{u}_{\mathrm{o}} −\frac{\mathrm{1}}{\mathrm{e}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}!} \\ $$$$\mathrm{u}_{\mathrm{o}} =\mathrm{A}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}=\left[−\mathrm{e}^{−\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}+\mathrm{1}\:} \:\frac{\mathrm{1}}{\mathrm{k}!} \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{n}!\mathrm{u}_{\mathrm{n}} =\mathrm{n}!\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{e}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}!}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com