if a_(n+1) = (√(a_1 + a_n )) find lim_(x→∞) a


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 147529 by mathdanisur last updated on 21/Jul/21

$i f a_{n + 1} = \sqrt{a_{1} + a_{n}}$ $Double subscripts: use braces to clarify$
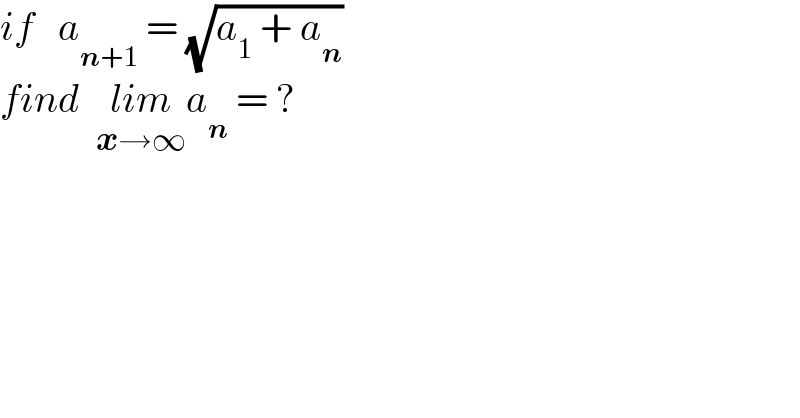
Commented by mathdanisur last updated on 21/Jul/21

$S o r r y a_{1} = 12$
	Answered by gsk2684 last updated on 21/Jul/21

	$L = \lim_{n \to \infty} a_{n + 1} = \lim_{n \to \infty} \sqrt{a_{1} + a_{n}} > 0$ $L = \sqrt{a_{1} + L}$ $L^{2} - L - a_{1} = 0$ $L = \frac{1 \pm \sqrt{1 + 4 a_{1}}}{2} > 0$ $L = \frac{1 + \sqrt{1 + 4 a_{1}}}{2} = \frac{1 + \sqrt{1 + 48}}{2} = 4$
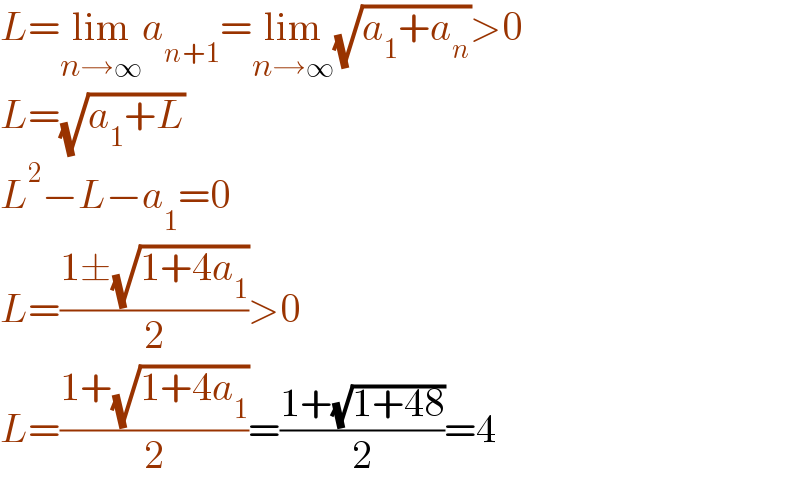
	Commented by Snail last updated on 21/Jul/21

	$Y o u a r e t e c h n i c a l l y w r o n g i n t h e s e c o n d l i n e$ $w h i l e w r i t i n g L u h a v d t o s h o w a t f i r s t t h e s e q$ $i s e i t h e r m o n o t o n i c i n c r e a s i n g o r d e c r e a s i n g$
	Answered by Snail last updated on 21/Jul/21

	$C l a i m a_{n + 1} ⩾ a_{n}$ $G o t h r o u g h b a s i c s t e p s o f i n d u c t i o n$ $a n d t h e n$ $F o r (m + 1) c a s e$ $w e h a v e a_{m + 1} ⩾ a_{m}$ $\sqrt{(} a_{1} + a_{m + 1}) ⩾ \sqrt{(} a_{1} + a_{m})$ $a_{m + 2} ⩾ a_{m} h e n c e t h e s e q i s m o n o t o n i c i n c r e a s$ $N o w u c a n d o a s l i k e i t i s d o n e$
	Commented by gsk2684 last updated on 21/Jul/21

	$y e s, t h a n k y o u$
	Answered by mathmax by abdo last updated on 21/Jul/21

	$a_{n + 1} = f (a_{n}) with f (x) = \sqrt{x + 12} (a_{1} = 12)$ $f is defined continue on [- 12, + \infty [$ $f^{^{'}} (x) = \frac{1}{2 \sqrt{x + 12}} > 0 \Rightarrow f is increazing on] - 12, + \infty [$ $so \lim_{n \to + \infty} a_{n} = x_{0} / f (x_{0}) = x_{0} (fix point of f)$ $\Rightarrow x_{0} = \sqrt{x_{0} + 12} \Rightarrow x_{0}^{2} - x_{0} - 12 = 0$ $Δ = 1 + 4 (12) = 49 \Rightarrow x_{1} = \frac{1 + 7}{2} = 4 and x_{2} = \frac{1 - 7}{2} = - 3 < 0$ $let prove [that a_{n} > 0 \forall n$ $a_{2} = \sqrt{a_{1} + 12} > 0 (true) let suppose a_{n} > 0 \Rightarrow$ $a_{n + 1} = \sqrt{a_{n} + 12} > 0 \Rightarrow \lim_{n \to + \infty} a_{n} = 4$
	Commented by mathdanisur last updated on 21/Jul/21

	$t h a n k y o u S i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum